题目内容
已知函数 (
(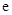 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求函数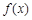 的单调区间;
的单调区间;
(Ⅱ)当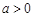 时,若
时,若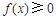 对任意的
对任意的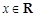 恒成立,求实数
恒成立,求实数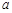 的值;
的值;
(Ⅲ)求证: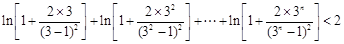 .
.
【答案】
(Ⅰ)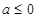 时,
时, 单调递增区间为
单调递增区间为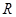 ;
; 时,
时, 单调递减区间为
单调递减区间为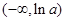 ,
,
单调递增区间为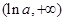 ;(Ⅱ)
;(Ⅱ)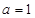 ; (Ⅲ)证明见解析
; (Ⅲ)证明见解析
【解析】
试题分析:(Ⅰ)利用导数分析函数的单调性,根据 和
和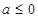 分类讨论得出函数的单调区间;(Ⅱ)先由(Ⅰ)中
分类讨论得出函数的单调区间;(Ⅱ)先由(Ⅰ)中 时的单调性可知
时的单调性可知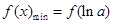 ,即
,即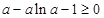 ,构造函数
,构造函数 ,由导函数分析可得
,由导函数分析可得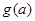 在
在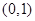 上增,在
上增,在 上递减,则
上递减,则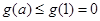 ,由
,由 对任意的
对任意的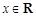 恒成立,故
恒成立,故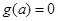 ,得
,得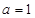 ;(Ⅲ)先由(Ⅱ)
;(Ⅲ)先由(Ⅱ) ,即
,即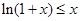
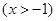 ,从而问题等价转化为证
,从而问题等价转化为证 .
.
试题解析:(Ⅰ)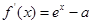 1分
1分
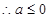 时,
时,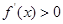 ,
, 在
在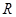 上单调递增。
2分
上单调递增。
2分
 时,
时, 时,
时,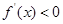 ,
, 单调递减,
单调递减,
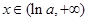 时,
时,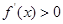 ,
, 单调递增.
4分
单调递增.
4分
(Ⅱ)由(Ⅰ), 时,
时,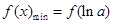
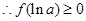 5分
5分
即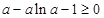 ,记
,记

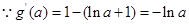
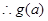 在
在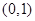 上增,在
上增,在 上递减
上递减
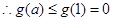
故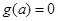 ,得
,得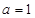 8分
8分
(Ⅲ)由(Ⅱ) ,即
,即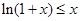
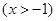 ,则
,则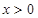 时,
时,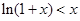
要证原不等式成立,只需证: ,即证:
,即证: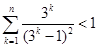
下证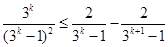 ①
9分
①
9分
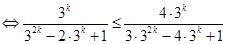
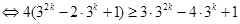

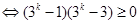
①中令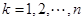 ,各式相加,得
,各式相加,得
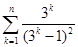
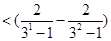
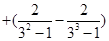
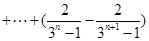
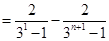
 成立,
成立,
故原不等式成立. 14分
方法二: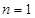 时,
时,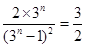
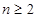 时,
时,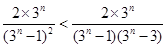
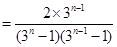
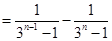
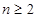 时,
时,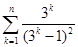
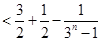
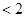
考点:1.利用导数数求函数的单调性;2.利用导数处理不等式的恒成立问题;3.等价转化的数学思想方法

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 其中
其中 为自然对数的底数,
为自然对数的底数,  .
. ,求函数
,求函数 的最值;
的最值; ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围. .(
.( 为自然对数的底)
为自然对数的底) 的最小值;
的最小值; 使得
使得 对于任意的正数
对于任意的正数 恒成立?若存在,求出
恒成立?若存在,求出 .e为自然对数的底
.e为自然对数的底 时取得最小值,求
时取得最小值,求 的值;
的值; ,求函数
,求函数 在点P
在点P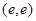 处的切线方程
处的切线方程 其中
其中 为自然对数的底数
为自然对数的底数 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围; 时,求函数
时,求函数 的极小值。
的极小值。