题目内容
已知函数 .(
.( 为自然对数的底)
为自然对数的底)
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)是否存在常数 使得
使得 对于任意的正数
对于任意的正数 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(Ⅰ)解:由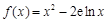 ,得
,得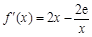
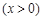 .
.
令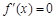 ,得
,得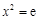 ,所以
,所以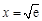 .
2分
.
2分
当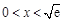 时,
时,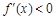 ,所以
,所以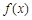 在
在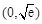 内是减函数;
内是减函数;
当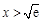 时,
时,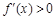 ,所以
,所以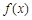 在
在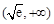 内是增函数.
2分
内是增函数.
2分
故函数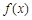 在
在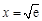 处取得最小值
处取得最小值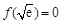 .
2分
.
2分
(Ⅱ)证明:由(Ⅰ)知,当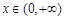 时,有
时,有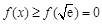 ,
,
即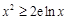 ,当且仅当
,当且仅当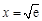 时,等号成立.
时,等号成立.
即两曲线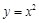 ,
,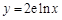 有唯一公共点
有唯一公共点 .
3分
.
3分
若存在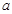 ,
,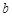 ,则直线
,则直线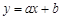 是曲线
是曲线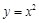 和
和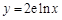 的公切线,切点为
的公切线,切点为 . 3分
. 3分
由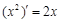 ,得直线
,得直线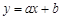 的斜率为
的斜率为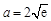 .
.
又直线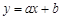 过点
过点 ,所以
,所以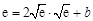 ,得
,得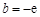 .
.
故存在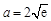 ,
,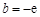 ,使得
,使得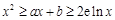 对于任意正数
对于任意正数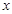 恒成立. 3分
恒成立. 3分
【解析】略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
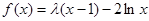 ,
, ,(
,( 为自然对数的底数).
为自然对数的底数). 时,求函数
时,求函数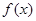 的单调区间;
的单调区间;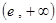 上恒为正数,求
上恒为正数,求 的最小值;
的最小值;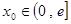 ,在
,在 上总存在两个不同的
上总存在两个不同的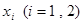 ,使得
,使得 成立,求
成立,求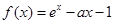 (
(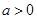 ,
,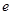 为自然对数的底数).
为自然对数的底数).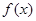 的最小值;
的最小值;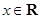 恒成立,求实数
恒成立,求实数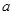 的值;
的值;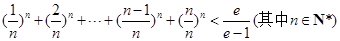
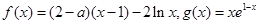 ,(
,( 为自然对数的底数)。
为自然对数的底数)。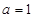 时,求函数
时,求函数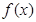 在区间
在区间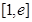 上的最大值和最小值;
上的最大值和最小值; 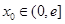 ,在
,在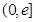 上总存在两个不同的
上总存在两个不同的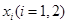 ,使得
,使得 成立,求
成立,求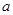 的取值范围。
的取值范围。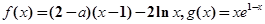 ,(
,(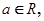 e为自然对数的底数)
e为自然对数的底数)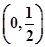 上无零点,求a的最小值;
上无零点,求a的最小值;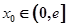 ,在
,在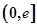 上总存在两个不同的
上总存在两个不同的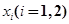 ,使得
,使得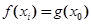 成立,求a的取值范围.
成立,求a的取值范围.