题目内容
已知函数 其中
其中 为自然对数的底数
为自然对数的底数
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)若函数 为单调函数,求实数
为单调函数,求实数 的取值范围;
的取值范围;
(3)若 时,求函数
时,求函数 的极小值。
的极小值。
【答案】
18.解:
(I)由
得 ,
,

(II)由 ,
,
∴数列{ }是以S1+1=2为首项,以2为公比的等比数列,
}是以S1+1=2为首项,以2为公比的等比数列,

 当n=1时a1=1满足
当n=1时a1=1满足
(III) ①
①
 ,②
,②
①-②得 ,
,
则 .
. 
 当n=1时,
当n=1时,
即当n=1或2时, 当n>2时,
当n>2时,
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 其中
其中 为自然对数的底数,
为自然对数的底数,
 .(Ⅰ)设
.(Ⅰ)设 ,求函数
,求函数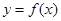 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问中,当 时,
时, ,
, .结合表格和导数的知识判定单调性和极值,进而得到最值。
.结合表格和导数的知识判定单调性和极值,进而得到最值。
第二问中,∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即
分离参数的思想求解参数的范围
解:(Ⅰ)当 时,
时, ,
, .
.
当 在
在 上变化时,
上变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
1/e |
∴ 时,
时, ,
, .
.
(Ⅱ)∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即 .
.
∴对于任意的 ,原不等式恒成立,等价于
,原不等式恒成立,等价于 对
对 恒成立,
恒成立,
∵对于任意的 时,
时, 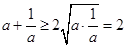 (当且仅当
(当且仅当 时取等号).
时取等号).
∴只需 ,即
,即 ,解之得
,解之得 或
或 .
.
因此, 的取值范围是
的取值范围是
 (
( 为常数,
为常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与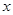 轴平行.
轴平行. 的单调区间;
的单调区间; ,其中
,其中 为
为 .
.