题目内容
19.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…其中从第三个数起,每一个数都等于他前面两个数的和.该数列是一个非常美丽、和谐的数列,有很多奇妙的属性,比如:随着数列项数的增加,前一项与后一项之比越逼近黄金分割0.6180339887.人们称该数列为{an}“斐波那契数列”,若把该数列{an}的每一项除以4所得的余数按相对应的顺序
组成新数列{bn},在数列{bn}中第2015项的值是1.
分析 根据数列,得到余数构成是数列是周期数列,即可得到结论.
解答 解:1,1,2,3,5,8,13,…除以4所得的余数分别为1,1,2,3,1,0,;1,1,2,3,1,0…,
即新数列{bn}是周期为6的周期数列,所以b2015=b235×6+5=b5=1,
故答案为:1.
点评 本题主要考查数列的应用,利用条件推导数列为周期数列是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.对于任意两个自然数m,n,定义某种?运算如下:当m,n都为奇数或偶数时,m?n=m+n;当m,n中一个为偶数,另一个为奇数时,m?n=mn.则在此定义下,集合M={(a,b)|a?b=18,a∈N,b∈N}中的元素个数为( )
| A. | 26 | B. | 25 | C. | 24 | D. | 23 |
9.经过如图程序,变量y的值为( )
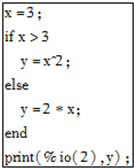
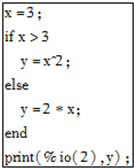
| A. | 3 | B. | 6 | C. | 9 | D. | 27 |
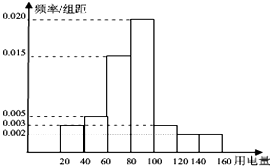 如图,是某市1000户居民月平均用电量的频率分布直方图,
如图,是某市1000户居民月平均用电量的频率分布直方图,