题目内容
3.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点垂直于双曲线实轴的直线交双曲线于P,Q两点,我们称线段PQ为双曲线的通径,若双曲线通径长是焦距的两倍,则此双曲线的离心率是( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\sqrt{5}+1$ | C. | $\frac{\sqrt{2}+1}{2}$ | D. | $\sqrt{2}+1$ |
分析 求出PQ的长,利用线段PQ的长度是焦距的两倍,可得$\frac{{b}^{2}}{a}$=2c,从而可求双曲线的离心率.
解答 解:不妨设P(c,y0),代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得y0=±$\frac{{b}^{2}}{a}$.
∵线段PQ的长度是焦距的两倍,
∴$\frac{{b}^{2}}{a}$=2c,
∴c2-a2=2ac,
∴e2-2e-1=0,
∵e>1,
∴e=1+$\sqrt{2}$.
故选:D.
点评 本题考查双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
11.已知函数$\left\{\begin{array}{l}{x+k(1-{a}^{2}),(x≥0)}\\{{x}^{2}-4x+(3-a)^{2},(x<0)}\end{array}\right.$,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的取值范围为( )
| A. | k≤0 | B. | k≥8 | C. | 0≤k≤8 | D. | k≤0或k≥8 |
12.集合M={x|$\frac{x}{x-1}$>0},集合N={x|y=$\sqrt{x}$},则M∩N等于( )
| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (0,1)∪(1,+∞) |
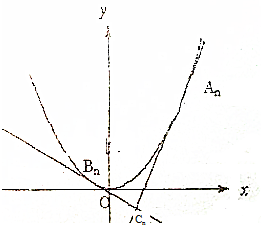 已知点An(xn,yn),Bn(sn,tn)(n∈N*)是抛物线x2=4y上不同的两点,设抛物线在点An,Bn,处的两条切线相互垂直,垂足为点Cn;
已知点An(xn,yn),Bn(sn,tn)(n∈N*)是抛物线x2=4y上不同的两点,设抛物线在点An,Bn,处的两条切线相互垂直,垂足为点Cn;