题目内容
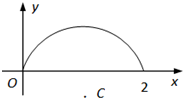 已知函数y=f(x)(x∈(0,2))的图象是如图所示的圆C的一段圆弧.现给出如下命题:
已知函数y=f(x)(x∈(0,2))的图象是如图所示的圆C的一段圆弧.现给出如下命题:①f′(1)=0;
②f′(x)≥0;
③f′(x)为减函数;
④若f′(a)+f′(b)=0,则a+b=2.
其中所有正确命题的序号为
①③④
①③④
.分析:对于①根据导数的几何意义,f′(1)表示函数f(x)在x=1处切线的斜率,由图可知其正确性;对于②由于函数f(x)在区间(1,2)上是减函数,根据导数的符号与单调性的关系知②不正确;对于③根据导数的几何意义,f′(x)表示函数f(x)在点(x,y)处切线的斜率,切线的斜率从正数→0→负数,且是渐渐变大的,从而进行判断;对于④若f′(a)+f′(b)=0,说明点x=a与x=b关于直线x=1对称,结合中点坐标公式可得结果.
解答:解:①根据导数的几何意义,f′(1)表示函数f(x)在x=1处切线的斜率,由图可知,函数f(x)在x=1处切线平行于x轴,故f′(1)=0,正确;
②由于函数f(x)在区间(1,2)上是减函数,故当x∈(1,2)时,f'(x)<0,故②不正确;
③根据导数的几何意义,f′(x)表示函数f(x)在点(x,y)处切线的斜率,由图可知,切线的斜率从正数→0→负数,且是渐渐变大的,故f′(x)为减函数,正确;
④若f′(a)+f′(b)=0,说明点x=a与x=b关于直线x=1对称,由中点坐标公式得
=1,则a+b=2,正确.
故答案为:①③④.
②由于函数f(x)在区间(1,2)上是减函数,故当x∈(1,2)时,f'(x)<0,故②不正确;
③根据导数的几何意义,f′(x)表示函数f(x)在点(x,y)处切线的斜率,由图可知,切线的斜率从正数→0→负数,且是渐渐变大的,故f′(x)为减函数,正确;
④若f′(a)+f′(b)=0,说明点x=a与x=b关于直线x=1对称,由中点坐标公式得
| a+b |
| 2 |
故答案为:①③④.
点评:本题考查命题的真假判断和应用,解题时要熟练掌握导函数的图象和性质.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足