题目内容
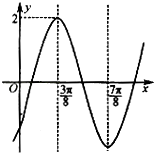
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() )的图象如图所示,直线x=
)的图象如图所示,直线x= ![]() ,x=
,x= ![]() 是其两条对称轴.
是其两条对称轴. 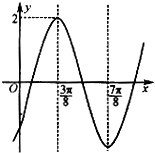
(1)求函数f(x)的解析式及单调区间;
(2)若f(α)= ![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:由题意, ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,∴T=π;
,∴T=π;
又∵ω>0,∴ω=2,
∴f(x)=2sin(2x+φ);
∵f( ![]() )=2sin(
)=2sin( ![]() +φ)=2,
+φ)=2,
∴解得φ=2kπ﹣ ![]() (k∈Z);
(k∈Z);
又∵﹣ ![]() <φ<
<φ< ![]() ,∴φ=﹣
,∴φ=﹣ ![]() ,
,
∴f(x)=2sin(2x﹣ ![]() );
);
∵2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() (k∈Z),
(k∈Z),
∴kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() (k∈Z),
(k∈Z),
∴函数f(x)的单调增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
(2)解:解法1:依题意得,2sin(2α﹣ ![]() )=
)= ![]() ,即sin(2α﹣
,即sin(2α﹣ ![]() )=
)= ![]() ,
,
∵ ![]() <α<
<α< ![]() ,∴0<2α﹣
,∴0<2α﹣ ![]() <
< ![]() ;
;
∴cos(2α﹣ ![]() )=
)= ![]() =
= ![]() ,
,
f( ![]() +α)=2sin[(2α﹣
+α)=2sin[(2α﹣ ![]() )+
)+ ![]() ];
];
∵sin[(2α﹣ ![]() )+
)+ ![]() ]=sin(2α﹣
]=sin(2α﹣ ![]() )cos
)cos ![]() +cos(2α﹣
+cos(2α﹣ ![]() )sin
)sin ![]()
= ![]() (
( ![]() +
+ ![]() )=
)= ![]() ,
,
∴f( ![]() +α)=
+α)= ![]() .
.
解法2:依题意得,sin(2α﹣ ![]() )=
)= ![]() ,得sin2α﹣cos2α=
,得sin2α﹣cos2α= ![]() ,①
,①
∵ ![]() <α<
<α< ![]() ,∴0<2α﹣
,∴0<2α﹣ ![]() <
< ![]() ,
,
∴cos(α﹣ ![]() )=
)= ![]() =
= ![]() ,
,
由cos(2α﹣ ![]() )=
)= ![]() 得,sin2α+cos2α=
得,sin2α+cos2α= ![]() ;②
;②
① +②得,2sin2α= ![]() ,
,
∴f( ![]() +α)=
+α)= ![]() .(
.(
解法3:由sin(2α﹣ ![]() )=
)= ![]() 得,sin2α﹣cos2α=
得,sin2α﹣cos2α= ![]() ,
,
两边平方得,1﹣sin4α ![]() ,∴sin4α=
,∴sin4α= ![]() ,
,
∵ ![]() <α<
<α< ![]() ,∴
,∴ ![]() <4α<
<4α< ![]() ,∴cos4α=﹣
,∴cos4α=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴sin22α= ![]() =
= ![]() ;
;
又∵ ![]() <2α<
<2α< ![]() ,∴sin2α=
,∴sin2α= ![]() ,
,
∴f( ![]() +α)=
+α)= ![]() .
.
【解析】(1)根据函数的图象求出T、ω和φ的值,即得f(x),再求出f(x)的单调增区间;(2)解法1:由sin(2α﹣ ![]() )求出cos(2α﹣
)求出cos(2α﹣ ![]() )的值,利用两角和的公式计算f(
)的值,利用两角和的公式计算f( ![]() +α)的值;解法2:由sin(2α﹣
+α)的值;解法2:由sin(2α﹣ ![]() )得sin2α﹣cos2α的值,cos(α﹣
)得sin2α﹣cos2α的值,cos(α﹣ ![]() )得cos(2α﹣
)得cos(2α﹣ ![]() )即sin2α+cos2α的值,计算出f(
)即sin2α+cos2α的值,计算出f( ![]() +α)的值;解法3:由sin(2α﹣
+α)的值;解法3:由sin(2α﹣ ![]() )得sin2α﹣cos2α的值,再得sin4α的值,再求出sin2α的值,从而求出f(
)得sin2α﹣cos2α的值,再得sin4α的值,再求出sin2α的值,从而求出f( ![]() +α)的值.
+α)的值.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案