题目内容
19．设α∈R，f（x）=a-$\frac{2}{{2}^{x}+1}$（x∈R）．（1）证明对任意实数a，f（x）为增函数．
（2）试确定a的值，使f（x）≤0恒成立．
分析 （1）由单调性的定义，注意作差、变形和定符号、下结论；
（2）由题意可得a≤$\frac{2}{{2}^{x}+1}$恒成立，运用指数函数的值域，求得右边函数的范围，即可得到a的范围．
解答 解：（1）证明：设m＜n，则f（m）-f（n）=a-$\frac{2}{{2}^{m}+1}$-（a-$\frac{2}{{2}^{n}+1}$）
=$\frac{2（{2}^{m}-{2}^{n}）}{（1+{2}^{m}）（1+{2}^{n}）}$，由m＜n，可得0＜2m＜2n，
即有f（m）＜f（n），则对任意实数a，f（x）为R上的增函数；
（2）f（x）≤0恒成立，即为a≤$\frac{2}{{2}^{x}+1}$恒成立，
由$\frac{2}{{2}^{x}+1}$在R上递减，且2x＞0，可得$\frac{2}{{2}^{x}+1}$∈（0，2），
则a≤0，即a的范围是（-∞，0]．
点评 本题考查函数的单调性的证明，注意运用单调性的定义，考查不等式恒成立问题的解法运用参数分离，考查运算能力，属于中档题．
练习册系列答案
相关题目
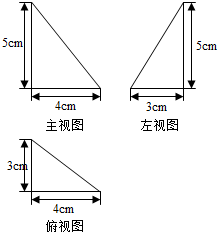如图是一个空间几何体的三视图，则这个几何体的外接球的体积是$\frac{125\sqrt{2}}{3}π$cm3．