题目内容
已知函数 =
= .
.
(Ⅰ)当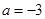 时,求不等式
时,求不等式  ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【答案】
(Ⅰ)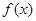 ≥3的解集为{
≥3的解集为{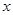 |
|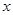 ≤1或
≤1或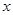 ≥4};(Ⅱ) [-3,0].
≥4};(Ⅱ) [-3,0].
【解析】
试题分析:(Ⅰ)当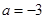 时,
时,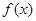 =
=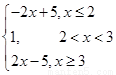 ,
,
当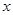 ≤2时,由
≤2时,由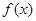 ≥3得
≥3得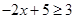 ,解得
,解得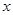 ≤1;
≤1;
当2<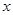 <3时,
<3时,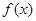 ≥3,无解;当
≥3,无解;当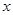 ≥3时,由
≥3时,由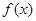 ≥3得
≥3得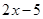 ≥3,解得
≥3,解得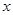 ≥4,
≥4,
∴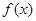 ≥3的解集为{
≥3的解集为{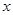 |
|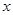 ≤1或
≤1或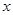 ≥4};
≥4};
(Ⅱ) 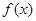 ≤
≤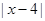
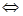
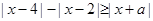 ,
,
当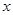 ∈[1,2]时,
∈[1,2]时,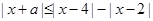 =
=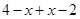 =2,
=2,
∴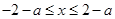 ,有条件得
,有条件得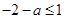 且
且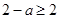 ,即
,即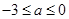 ,
,
故满足条件的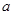 的取值范围为[-3,0].
的取值范围为[-3,0].
考点:本题考查了绝对值不等式的运用
点评:在解答含有绝对值不等式问题时,要注意分段讨论来取绝对值符号的及利用绝对值的几何意义来求含有多个绝对值的最值问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|