题目内容
12.已知函数f(x)是定义在R上的偶函数,且f(x+2)=-f(x),若$f(\frac{1}{2})=0$,则方程f(x)=0在区间(0,4)内解的个数的最小值是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据函数奇偶性的性质,结合函数周期性,即可得到结论.
解答 解:∵f(x)是偶函数,且若$f(\frac{1}{2})=0$,
∴若f(-$\frac{1}{2}$)=$f(\frac{1}{2})=0$,
∵f(x+2)=-f(x),
∴函数f(x+4)=f(x),
则f(-$\frac{1}{2}$+4)=f($\frac{7}{2}$)=f(-$\frac{1}{2}$)=0,
∴f($\frac{1}{2}+2$)=-f($\frac{1}{2}$)=0,
即f($\frac{5}{2}$)=0,f(-$\frac{1}{2}+2$)=-f(-$\frac{1}{2}$)=0,
即f($\frac{3}{2}$)=0,
f($\frac{3}{2}$+2)=-f($\frac{3}{2}$)=0,即f($\frac{5}{2}$)=0,
则f(-$\frac{5}{2}$)=f($\frac{5}{2}$)=0,
则在区间(0,4)内,
有f($\frac{1}{2}$)=0,f($\frac{3}{2}$)=0,f($\frac{5}{2}$)=0,f($\frac{7}{2}$)=0,
故至少有4个根,
故选:C
点评 本题主要考查函数根的格式的判断,根据函数奇偶性和周期性之间的关系进行递推是解决本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
2.已知集合M={x|9x${\;}^{{\;}^{2}}$<27x},N={x|log${\;}_{\frac{1}{2}}$(x-1)>0},则M∩N=( )
| A. | (0,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,2) | C. | (1,$\frac{3}{2}$) | D. | (0,1) |
3.已知命题p:“直线l垂直于平面α内的无数条直线”的充要条件是“l⊥α”;命题q:若平面α⊥平面β,直线a?β,则“a⊥α”是“a平行于β”的充分不必要条件,则正确命题是( )
| A. | p∧q | B. | (¬p)∧q | C. | (?p)∧(¬q) | D. | p∨(¬q) |
17.已知集合A={x|0<x<5},B={x|x2-2x-3>0},则A∩B=( )
| A. | (0,3) | B. | (3,5) | C. | (-1,0) | D. | (0,3] |
2.已知全集U=R,集合A={x|x2>2x+3},B={x|log3x>1},则下列关系正确的是( )
| A. | A∪∁UB=R | B. | B∪∁UA=R | C. | A∪B=R | D. | A∩B=A |
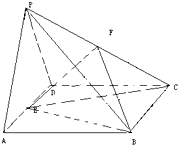 如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,
如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,