题目内容
已知在梯形ABCD中，AB∥DC，且A、B、D三点的坐标分别为（0，0）、（2，0）、（1，1），则顶点C的横坐标的取值范围是
（1，3）∪（3，+∞）
（1，3）∪（3，+∞）
．分析：根据梯形的性质AB∥DC，且AB≠DC，易得向量
∥
，结合向量平行的坐标运算，构造不等式，即可得到C点横坐标的取值范围．
| AB |
| CD |
解答：解：当ABCD为平行四边形，
则
=
+
=（2，0）+（1，1）=（3，1），
故满足题意的顶点C的横坐标的取值范围是（1，3）∪（3，+∞）
故答案为：（1，3）∪（3，+∞）．
则
| AC |
| AB |
| AD |
故满足题意的顶点C的横坐标的取值范围是（1，3）∪（3，+∞）
故答案为：（1，3）∪（3，+∞）．
点评：利用向量证明平面内线与线的位置关系，是向量的主要用法，当我们需要判断一个四边形的形状时，也常常使用平面向量的解答或证明，若两个向量平行，则表示它们的有向线段所在的直线平行或重合，若两个向量的模相等，则表示它们的有向线段长度相等．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
如图，已知在梯形ABCD中，AB∥DC，且AB=2CD，E、F分别是DC、AB的中点，设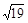
，∠BAD＝
，求梯形的高.