题目内容
如图，已知在梯形ABCD中，AB∥DC，且AB=2CD，E、F分别是DC、AB的中点，设| AD |
| a |
| AB |
| b |
| a |
| b |
| DC |
| BC |
| EF |
分析：根据向量共线和条件用
表示出
，向量加法的三角形法则和线段的关系依次表示出
和
．
| b |
| DC |
| BC |
| EF |
解答：解：∵AB∥DC且AB=2CD，
∴
=
=
．
由向量加法的三角形法则，
有
=
+
+
=-
+
+
=
-
．
同理，
=
+
+
=
-
-
=
-
．
∴
| DC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| b |
由向量加法的三角形法则，
有
| BC |
| BA |
| AD |
| DC |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
同理，
| EF |
| EC |
| CB |
| BF |
| 1 |
| 2 |
| DC |
| BC |
| 1 |
| 2 |
| AB |
| 1 |
| 4 |
| b |
| a |
点评：本题主要考查了向量加减、数乘混合运算及其几何意义，用一组向量来表示一个向量，是以后解题过程中常见到的，向量的加减运算是用向量解决问题的基础，熟练掌握．
练习册系列答案
全能测控期末小状元系列答案
相关题目
=
，
=
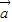，试用
，
为基底表示
、
、
．