题目内容
【题目】已知函数f(x)= ![]() (x∈R)时,则下列所有正确命题的序号是 .
(x∈R)时,则下列所有正确命题的序号是 .
①若任意x∈R,则等式f(﹣x)+f(x)=0恒成立;
②存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根;
③任意x1 , x2∈R,若x1≠x2 , 则一定有f(x1)≠f(x2)
④存在k∈(1,+∞),使得函数g(x)=f(x)﹣kx在R上有三个零点.
【答案】①②③
【解析】解:f(x)= ![]() (x∈R)的图象为对于①,函数的定义域为R,f(﹣x)=
(x∈R)的图象为对于①,函数的定义域为R,f(﹣x)= ![]() =﹣
=﹣ ![]() =﹣f(x),
=﹣f(x),
f(x)+f(﹣x)=0恒成立,故①正确,
对于②,由图象可知,函数的值域为(﹣1,1),
故存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根,故②正确,
对于③由图象可知,函数在R上单调递增,故任意x1 , x2∈R,若x1≠x2 , 则一定有f(x1)≠f(x2),故③正确,
对于④,分别画出y=f(x)与y=kx的图象,由图象可知,使得函数g(x)=f(x)﹣kx在R上有一个零点,故④错误,
所以答案是:①②③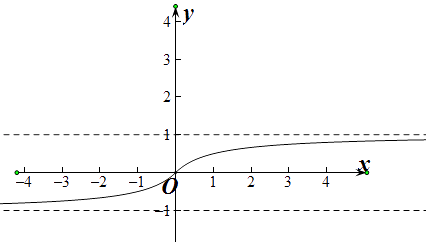

练习册系列答案
相关题目