题目内容
函数
的最大值是（ ）A．
B．1
C．
D．
【答案】分析：化简函数的解析式为-（cosx-2）2+
，再利用二次函数的性质求得函数的最大值．
解答：解：函数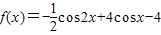
=-cos2x+4cosx-
=-（cosx-2）2+
，
故当cosx=1时，函数取得最大值为-
，
故选D．
点评：本题主要考查余弦函数的值域，二次函数的性质的应用，属于中档题．
，再利用二次函数的性质求得函数的最大值．解答：解：函数
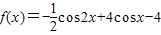=-cos2x+4cosx-=-（cosx-2）2+，故当cosx=1时，函数取得最大值为-
，故选D．
点评：本题主要考查余弦函数的值域，二次函数的性质的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知二次函数y=ax2+（a2+1）x在x=1处的导数值为1，则该函数的最大值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|