题目内容
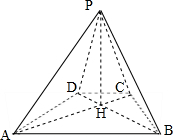
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高.
(Ⅰ)证明:平面PAC⊥平面PBD;
(Ⅱ)若
AB=,∠APB=∠ADB=60°,求四棱锥P-ABCD的体积.
分析:(Ⅰ)要证平面PAC⊥平面PBD,只需证明平面PAC内的直线AC,垂直平面PBD内的两条相交直线PH,BD即可.
(Ⅱ)
AB=,∠APB=∠ADB=60°,计算等腰梯形ABCD的面积,PH是棱锥的高,然后求四棱锥P-ABCD的体积.
解答:解:
(1)因为PH是四棱锥P-ABCD的高.
所以AC⊥PH,又AC⊥BD,PH,BD都在平PHD内,且PH∩BD=H.
所以AC⊥平面PBD.
故平面PAC⊥平面PBD(6分)
(2)因为ABCD为等腰梯形,AB∥CD,AC⊥BD,AB=
.
所以HA=HB=
.
因为∠APB=∠ADB=60°
所以PA=PB=
,HD=HC=1.
可得PH=
.
等腰梯形ABCD的面积为S=
ACxBD=2+
(9分)
所以四棱锥的体积为V=
×(2+
)×
=
.(12分)
点评:本题考查平面与平面垂直的判定,棱柱、棱锥、棱台的体积,考查空间想象能力,计算能力,推理能力,是中档题.
练习册系列答案
相关题目
 如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高.
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高.
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,