题目内容
在平面直角坐标系中,点P (-1,2 ) 关于x轴的对称点的坐标为【 】
| A.(-1,-2 ) | B.(1,-2 ) | C.(2,-1 ) | D.(-2,1 ) |
A
解析试题分析:
平面直角坐标系中任意一点P(x,y),关于x轴的对称点的坐标是(x,-y),即关于横轴的对称点,横坐标不变,纵坐标变成相反数,这样就可以求出对称点的坐标。解:点P(2,3)关于x轴的对称点的坐标是(2,-3).故选B
考点:关于轴对称点的特点
点评:本试题考查了关于轴对称的点的横坐标和纵坐标的特点,属于基础题。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
函数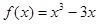 的递减区间是
的递减区间是
A. 或 或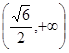 | B.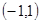 |
C.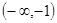 或 或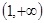 | D.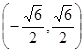 |
设 是连续的偶函数,且当
是连续的偶函数,且当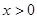 时,
时, 是单调函数,则满足
是单调函数,则满足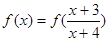 的所有
的所有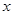 之和为( )
之和为( )
A.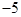 | B.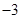 | C.5 | D.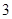 |
判断下列各组中的两个函数是同一函数的为( )
(1)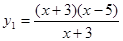 ,
,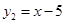 ;
;
(2)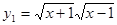 ,
,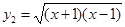 ;
;
(3)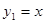 ,
,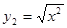 ;
;
(4)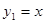 ,
,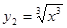 ;
;
(5)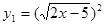 ,
, 。
。
| A.(1),(2) | B.(2),(3) | C.(4) | D.(3),(5) |
函数y=xlnx在区间 (0,1)上是 ( )
| A.单调增函数 |
| B.单调减函数 |
C.在(0,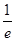 )上是减函数,在( )上是减函数,在(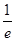 ,1)上是增函数 ,1)上是增函数 |
D.在(0,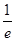 )上是增函数,在( )上是增函数,在(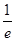 ,1)上是减函数 ,1)上是减函数 |
定义在R上的奇函数 在(0,+∞)上是增函数,又
在(0,+∞)上是增函数,又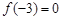 ,则不等式
,则不等式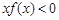 的解集为( )
的解集为( )
| A.(-3,0)∪(0,3) | B.(-∞,-3)∪(3,+∞) |
| C.(-3,0)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
函数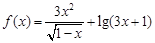 的定义域是
的定义域是
A.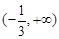 | B.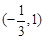 | C.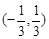 | D.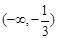 |
直线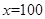 与函数
与函数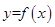 的图象的交点个数是 ( )
的图象的交点个数是 ( )
| A.0 | B.1 | C.0或1 | D.以上均不对 |
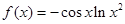 的部分图象大致是图中的( )
的部分图象大致是图中的( )