题目内容
直线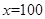 与函数
与函数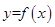 的图象的交点个数是 ( )
的图象的交点个数是 ( )
| A.0 | B.1 | C.0或1 | D.以上均不对 |
C
解析试题分析:根据函数的定义:定义域内每一个 对应唯一的
对应唯一的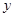 ,当
,当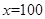 在定义域范围内时,有唯一解,当
在定义域范围内时,有唯一解,当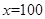 无定义时,没有解.
无定义时,没有解.
考点:函数的概念及其构成要素
点评:本题考查对函数的定义的理解,通过画图得出结论:直线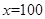 与函数
与函数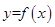 的图象至多有一个交点,属于基础题.本题易因为对函数概念理解不深导致错误.
的图象至多有一个交点,属于基础题.本题易因为对函数概念理解不深导致错误.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系中,点P (-1,2 ) 关于x轴的对称点的坐标为【 】
| A.(-1,-2 ) | B.(1,-2 ) | C.(2,-1 ) | D.(-2,1 ) |
已知函数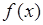 是定义在R上的奇函数,当
是定义在R上的奇函数,当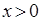 时,
时,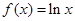 ,则
,则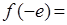 ( )
( )
| A.1 | B.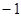 | C.2 | D.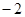 |
函数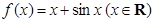 ( )
( )
A.是偶函数,且在 上是减函数 上是减函数 | B.是偶函数,且在 上是增函数 上是增函数 |
C.是奇函数,且在 上是减函数 上是减函数 | D.是奇函数,且在 上是增函数 上是增函数 |
已知奇函数f(x)列任意的正实数x1,x2(x1≠x2),恒有( ) (x1-x2)( (x1)-f(x2)>0),则一定正确的是
| A.f(4)>f(一6) | B.f(一4)<f(一6) |
| C.f(一4)>f(一6) | D.f(4)<f(一6) |
函数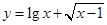 的定义域是( )
的定义域是( )
A.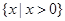 | B. | C.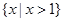 | D.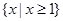 |
设函数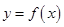 的定义域为
的定义域为 ,则函数
,则函数 和函数
和函数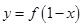 的图象关于( )
的图象关于( )
A.直线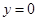 对称 对称 | B.直线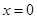 对称 对称 |
C.直线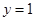 对称 对称 | D.直线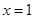 对称 对称 |
已知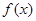 为定义在
为定义在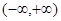 上的可导函数,且
上的可导函数,且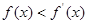 对于任意
对于任意 恒成立,则( )
恒成立,则( )
A.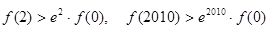 |
B.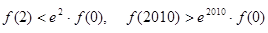 |
C.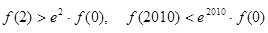 |
D.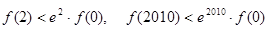 |
设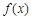 在
在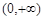 上是单调递增函数,当
上是单调递增函数,当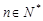 时,
时,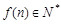 ,且
,且 ,则( )
,则( )
A.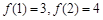 | B. |
C.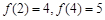  | D.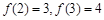 |