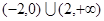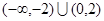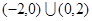题目内容
设 是连续的偶函数,且当
是连续的偶函数,且当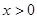 时,
时, 是单调函数,则满足
是单调函数,则满足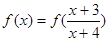 的所有
的所有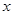 之和为( )
之和为( )
A.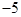 | B.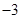 | C.5 | D.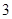 |
A
解析试题分析: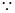
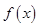 是偶函数
是偶函数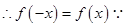
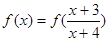
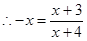
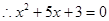 所有x的和为
所有x的和为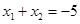
考点:函数性质:奇偶性单调性
点评:函数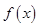 是偶函数则有
是偶函数则有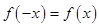 ,函数
,函数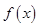 是奇函数则有
是奇函数则有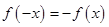 ,本题中当
,本题中当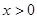 时,
时, 是单调函数,所以当
是单调函数,所以当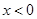 时函数也是单调函数,
时函数也是单调函数,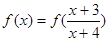 方可转化为
方可转化为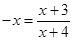

练习册系列答案
相关题目
已知函数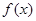 对定义域
对定义域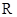 内的任意
内的任意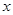 都有
都有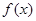 =
=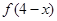 ,且当
,且当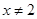 时其导函数
时其导函数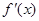 满足
满足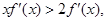 若
若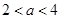 则
则
A.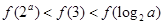 | B.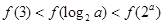 |
C.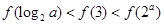 | D.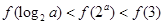 |
设函数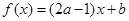 是
是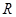 上的减函数,则有( )
上的减函数,则有( )
A.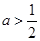 | B.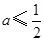 | C.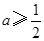 | D.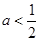 |
已知偶函数 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且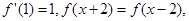 则曲线
则曲线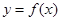 在
在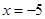 处的切线的斜率为 ( )
处的切线的斜率为 ( )
| A.2 | B.-2 | C.1 | D.-1 |
函数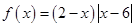 在
在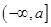 上取得最小值
上取得最小值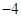 ,则实数
,则实数 的集合是( )
的集合是( )
A.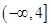 | B.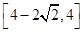 | C.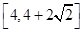 | D.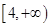 |
设f(x)是定义在R的偶函数,对任意xÎR,都有f(x-2)=f(x+2),且当xÎ[-2, 0]时, f(x)=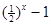 .若在区间(-2,6]内关于x的方程
.若在区间(-2,6]内关于x的方程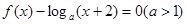 恰有3个不同的实数根,则实数a的取值范围是( )
恰有3个不同的实数根,则实数a的取值范围是( )
| A.(1, 2) | B.(2,+¥) | C.(1,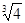 ) ) | D.(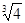 , 2) , 2) |
在平面直角坐标系中,点P (-1,2 ) 关于x轴的对称点的坐标为【 】
| A.(-1,-2 ) | B.(1,-2 ) | C.(2,-1 ) | D.(-2,1 ) |
已知函数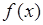 是定义在R上的奇函数,当
是定义在R上的奇函数,当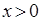 时,
时,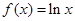 ,则
,则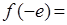 ( )
( )
| A.1 | B.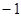 | C.2 | D.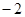 |
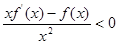 成立,则不等式
成立,则不等式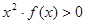 的解集是( )
的解集是( )