题目内容
【题目】已知数列{an}的通项公式为 an=(n﹣k1)(n﹣k2),其中k1,k2∈Z:
(1)试写出一组k1,k2∈Z的值,使得数列{an}中的各项均为正数;
(2)若k1=1、k2∈N*,数列{bn}满足bn=![]() ,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
(3)若0<k1<k2,数列{cn}满足cn=an+|an|,其前n项和为Sn,且使ci=cj≠0(i,j∈N*,i<j)的i和j有且仅有4组,S1、S2、…、Sn中至少3个连续项的值相等,其他项的值均不相等,求k1,k2的最小值.
【答案】(1)k1=k2=0(2)k2=7,8,9,10,11(3)k1的最小值为5,k2的最小值为6
【解析】
(1)通过函数![]() 是与
是与![]() 轴交于
轴交于![]() 两点且开口向上的抛物线可知,只需知
两点且开口向上的抛物线可知,只需知![]() 均在1的左边即可;
均在1的左边即可;
(2)通过![]() 化简可知
化简可知![]() ,排除
,排除![]() 可知
可知![]() ,此时可知对于
,此时可知对于![]() 而言,当
而言,当![]() 时
时![]() 单调递减,当
单调递减,当![]() 时
时![]() 单调递增,进而解不等式组
单调递增,进而解不等式组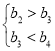 即得结论;
即得结论;
(3)通过![]() 及
及![]() 可知
可知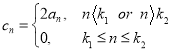 ,结合
,结合![]() 可知
可知![]() ,从而可知
,从而可知![]() 的最小值为5,通过
的最小值为5,通过![]() 中至少3个连续项的值相等可知
中至少3个连续项的值相等可知![]() ,进而可得
,进而可得![]() 的最小值为6.
的最小值为6.
解:(1)通过函数![]() 是与
是与![]() 轴交于
轴交于![]() 两点且开口向上的抛物线可知,只需知
两点且开口向上的抛物线可知,只需知![]() 均在1的左边即可,
均在1的左边即可,
故可取![]() ;
;
(2)![]() ,
,![]() ,
,
当![]() 时,
时,![]() 均单调递增,不合题意;
均单调递增,不合题意;
当![]() 时,对于
时,对于![]() 可知:
可知:
当![]() 时
时![]() 单调递减,当
单调递减,当![]() 时
时![]() 单调递增,
单调递增,
由题意可知![]() ,
,
联立不等式组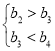 ,即
,即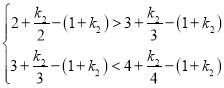 ,解得:
,解得:![]() ,
,![]() ;
;
(3)![]() ,
,
∴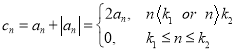 ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
此时![]() 的四个值为1,2,3,4,故
的四个值为1,2,3,4,故![]() 的最小值为5,
的最小值为5,
又![]() 中至少3个连续项的值相等,
中至少3个连续项的值相等,
不妨设![]() ,则
,则![]() ,
,
∵当![]() 时
时![]() ,
,![]() ,
,![]() ,即
,即![]() 的最小值为6.
的最小值为6.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目