Question

【题目】已知=（sinx，cosx），=（cosφ，sinφ）（|φ|＜）．函数

f（x）= 且f（－x）=f（x）．

（Ⅰ）求f（x）的解析式及单调递增区间；

（Ⅱ）将f（x）的图象向右平移单位得g（x）的图象，若g（x）+1≤ax+cosx在x∈[0， ]上恒成立，求实数a的取值范围．

Answer 1

【答案】（Ⅰ）f（x）=sin（x+），；（Ⅱ） .

【解析】试题分析：（1）利用向量的坐标运算得到，再由f（-x）=f（x）可知函数f（x）的图象关于直线x=对称，所以+φ=+kπ，进而得到φ=，利用三角函数的性质求解单调区间即可；

（2）将f（x）的图象向右平移单位得g（x）= sinx，即sinx+1≤ax+cosx在x∈[0，]上恒成立，利用数形结合分别研究h（x）=sinx-cosx和φ（x）= ax—1即可.

试题解析：

（Ⅰ）∵f（x）==sinxcosφ+cosxsinφ=sin（x+φ），

再由f（-x）=f（x）可知函数f（x）的图象关于直线x=对称，

∴+φ=+kπ，k∈Z，又|φ|＜，∴φ=

∴f（x）=sin（x+），

由2kπ-≤ x+≤2kπ+可得2kπ-≤x≤ 2kπ+，

∴函数的递增区间为[2kπ-，2kπ+]，k∈Z；

（Ⅱ）由图象平移易知g（x）=sinx，即sinx+1≤ax+cosx在x∈[0，]上恒成立．

也即sinx-cosx≤ax-1在x∈[0，]上恒成立.

令h（x）=sinx-cosx=sin（x-），x∈[0，]；

φ（x）= ax-1

如下图：h（x）的图象在φ（x）图象的下方，

则： a ≥kAB=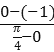=，故.