题目内容
【题目】如图，用35个单位正方形拼成一个矩形，点P1、P2、P3、P4以及四个标记为“▲”的点在正方形的顶点处，设集合Ω={P1 ， P2 ， P3 ， P4}，点P∈Ω，过P作直线lP ， 使得不在lP上的“▲”的点分布在lP的两侧．用D1（lP）和D2（lP）分别表示lP一侧和另一侧的“▲”的点到lP的距离之和．若过P的直线lP中有且只有一条满足D1（lP）=D2（lP），则Ω中所有这样的P为 ． 
【答案】P1、P3、P4
【解析】解：设记为“▲”的四个点为A，B，C，D，线段AB，BC，CD，DA的中点分别为E，F，G，H，
易知EFGH为平行四边形；如图所示，
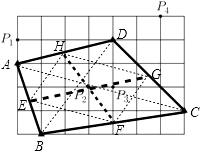
四边形ABCD两组对边中点的连线交于点P2，
即符合条件的直线lP一定经过点P2，
因此：经过点P2的直线有无数条；
同时经过点P1和P2的直线仅有1条，
同时经过点P3和P2的直线仅有1条，
同时经过点P4和P2的直线仅有1条，
所以符合条件的点为P1、P3、P4．
故答案为：P1、P3、P4．
根据任意四边形ABCD两组对边中点的连线交于一点，过此点作直线，让四边形的四个顶点不在该直线的同一侧，那么该直线两侧的四边形的顶点到直线的距离之和是相等的；由此得出结论．
练习册系列答案
相关题目
