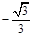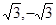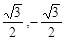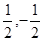题目内容
某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
(1该厂对这两种型号挖掘机有几种生产方案?
(2)该厂如何生产获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高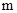 万元(
万元(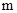 >0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
(2)该厂如何生产获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高
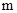 万元(
万元(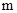 >0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)(1)①A型38台,B型62台;
②A型39台,B型61台;
③A型40台,B型60台.
(2)生产A型38台,B型62台时,获得最大利润.
(3)当m=10时,m-10=0则三种生产方案获得利润相等;
当m>10,则x=40时,W最大,即生产A型40台,B型60台
②A型39台,B型61台;
③A型40台,B型60台.
(2)生产A型38台,B型62台时,获得最大利润.
(3)当m=10时,m-10=0则三种生产方案获得利润相等;
当m>10,则x=40时,W最大,即生产A型40台,B型60台
试题分析:解:(1)设生产A型挖掘机x台,则B型挖掘机100-x台, 1分
由题意得22400≤200x+240(100-x)≤22500,
解得37.5≤x≤40. 3分
∵x取非负整数,
∴x为38,39,40.
∴有三种生产方案
①A型38台,B型62台;
②A型39台,B型61台;
③A型40台,B型60台. 5分
(2)设获得利润W(万元),由题意得W=50x+60(100-x)=6000-10x
∴当x=38时,W最大=5620(万元),
即生产A型38台,B型62台时,获得最大利润. 7分
(3)由题意得W=(50+m)x+60(100-x)=6000+(m-10)x
∴当0<m<10,则x=38时,W最大,即生产A型38台,B型62台;
当m=10时,m-10=0则三种生产方案获得利润相等;
当m>10,则x=40时,W最大,即生产A型40台,B型60台. 10分
点评:解决的关键是对于已知的变量来表示出代数式,然后借助于函数的性质来求解最值,属于基础题。

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
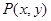 满足
满足 ,点Q(5,4)则
,点Q(5,4)则 的最小值是 。
的最小值是 。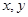 满足
满足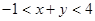 ,且
,且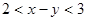 ,则
,则 的取值范围是________.
的取值范围是________.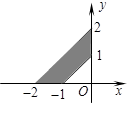
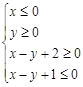
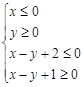

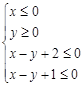
 的两条渐近线和直线
的两条渐近线和直线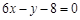 所围成三角形的边界及内部.当
所围成三角形的边界及内部.当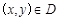 时,
时,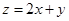 的最大值为( ).
的最大值为( ).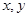 满足约束条件
满足约束条件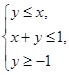 ,则
,则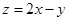 的最大值是
的最大值是  满足不等式组
满足不等式组 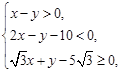 则
则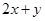 的最大值是( )
的最大值是( )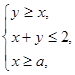 且z的最大值是最小值的4倍,则a的值是 .
且z的最大值是最小值的4倍,则a的值是 .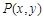 在圆
在圆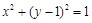 上运动,则
上运动,则 的最大值与最小值为( )
的最大值与最小值为( ) ,
,