题目内容
(本小题满分12分)
设数列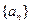 的前
的前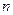 项和为
项和为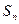 ,且
,且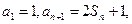 数列
数列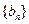 满足
满足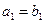 ,点
,点 在直线
在直线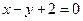 上,
上, .
.
(Ⅰ)求数列 ,
,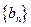 的通项公式;
的通项公式;
(Ⅱ)设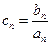 ,求数列
,求数列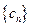 的前
的前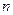 项和
项和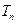 .
.
设数列
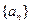 的前
的前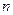 项和为
项和为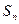 ,且
,且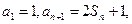 数列
数列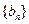 满足
满足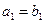 ,点
,点 在直线
在直线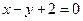 上,
上, .
.(Ⅰ)求数列
 ,
,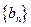 的通项公式;
的通项公式;(Ⅱ)设
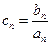 ,求数列
,求数列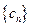 的前
的前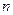 项和
项和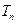 .
.(Ⅰ)
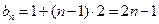
(Ⅱ)
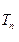
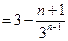
解:(Ⅰ)由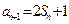 可得
可得 ,两式相
,两式相 减
减
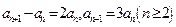 .
.
又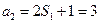 ,所以
,所以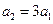 .
.
故 是首项为
是首项为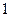 ,公比为
,公比为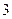 的等比数列. 所以
的等比数列. 所以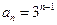 . --------(3分)
. --------(3分)
又由点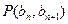 在直线
在直线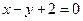 上,所以
上,所以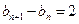 .
.
则数列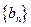 是首项为1,公差为2的等差数列.
是首项为1,公差为2的等差数列.
则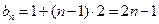 . -----------------------(6分)
. -----------------------(6分)
(Ⅱ)因为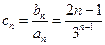 ,所以
,所以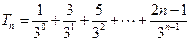 .
.
则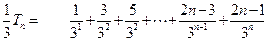 ,---(8分)
,---(8分)
两式相减得:
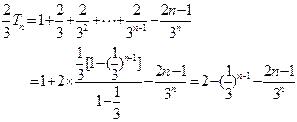 ------------
------------ (10分)
(10分)
所以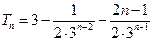
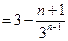 . --------------------(12分)
. --------------------(12分)
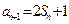 可得
可得 ,两式相
,两式相 减
减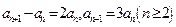 .
.又
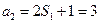 ,所以
,所以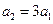 .
. 故
 是首项为
是首项为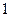 ,公比为
,公比为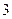 的等比数列. 所以
的等比数列. 所以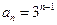 . --------(3分)
. --------(3分)又由点
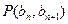 在直线
在直线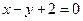 上,所以
上,所以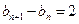 .
.则数列
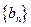 是首项为1,公差为2的等差数列.
是首项为1,公差为2的等差数列.
则
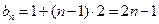 . -----------------------(6分)
. -----------------------(6分)(Ⅱ)因为
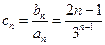 ,所以
,所以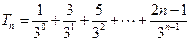 .
.则
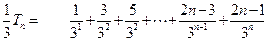 ,---(8分)
,---(8分)两式相减得:

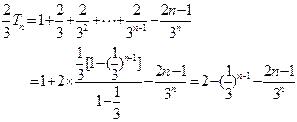 ------------
------------ (10分)
(10分)所以
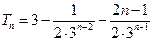
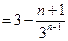 . --------------------(12分)
. --------------------(12分)
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 是由正数组成的等差数列,
是由正数组成的等差数列,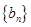 是由正数组成的等比数列,且
是由正数组成的等比数列,且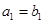 ,
,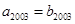 ,则必有 ( )
,则必有 ( )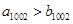
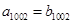
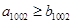
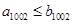

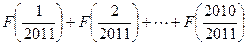 ;
; 满足
满足 ,求数列
,求数列 >
> 。
。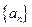 中,已知
中,已知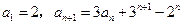
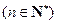 .
.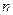 项和
项和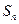 .
.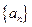 满足
满足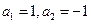 ,当
,当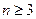 ,
,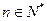 时,
时,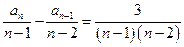 .
.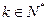 ,使得
,使得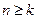 时,不等式
时,不等式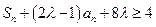 对任意实数
对任意实数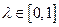 恒成立?若存在,求出
恒成立?若存在,求出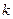 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. 轴上是否存在定点
轴上是否存在定点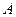 ,使得三点
,使得三点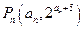 、
、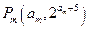 、
、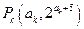 (其中
(其中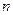 、
、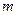 、
、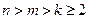 )到定点
)到定点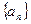 中,
中,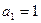 ,前10项和
,前10项和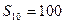 .
.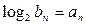 ,证明
,证明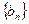 为等比数列,并求
为等比数列,并求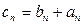 ,求
,求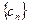 的前五项之和。
的前五项之和。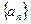 的前n项和为
的前n项和为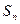 ,若
,若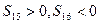 ,则
,则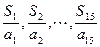 中最大的
中最大的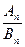 =
=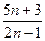 ,则
,则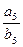 =
=