题目内容
(本题满分14分)
在数列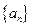 中,已知
中,已知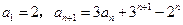
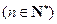 .
.
(1)求数列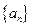 的通项公式;
的通项公式;
(2)求数列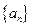 的前
的前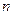 项和
项和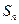 .
.
在数列
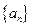 中,已知
中,已知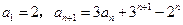
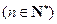 .
.(1)求数列
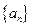 的通项公式;
的通项公式;(2)求数列
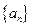 的前
的前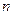 项和
项和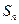 .
.、
(1)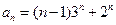
(3)数列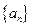 的前
的前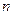 项和
项和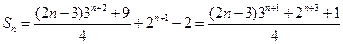
(1)
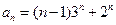
(3)数列
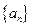 的前
的前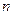 项和
项和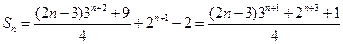
解:(1)解法1:由
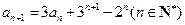
可得
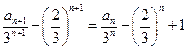 ,------------------------------3分
,------------------------------3分∴数列
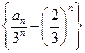 是首项为
是首项为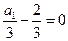 ,公差为1等差数列,
,公差为1等差数列,∴
 , -----------------6分
, -----------------6分∴数列
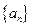 的通项公式为
的通项公式为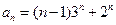 .-----------------------7分
.-----------------------7分解法2:由
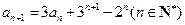
可得
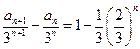 -------------------------2分
-------------------------2分令
 ,则
,则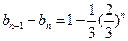 ---------------------3分
---------------------3分∴当
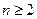 时
时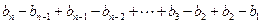
 ----5分
----5分
∴

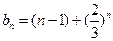 --------------------------------6分
--------------------------------6分∴
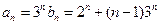 -------------------------------7分
-------------------------------7分解法3:∵
 , -------------1分
, -------------1分 ,-----------------------------------2分
,-----------------------------------2分 .---------------------------3分
.---------------------------3分由此可猜想出数列
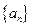 的通项公式为
的通项公式为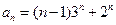 .----------------4分
.----------------4分以下用数学归纳法证明.
①当
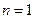 时,
时,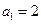 ,等式成立.
,等式成立.②假设当
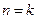 (
(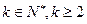 )时等式成立,即
)时等式成立,即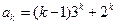 ,
,那么
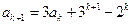

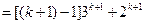 .--------------------------------6分
.--------------------------------6分这就是说,当
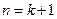 时等式也成立.根据①和②可知,等式
时等式也成立.根据①和②可知,等式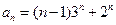 对任何
对任何 都成立.-------------------------------7分
都成立.-------------------------------7分(2)令
 , ------①-----8分
, ------①-----8分 ------②------9分
------②------9分①式减去②式得:
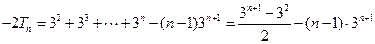 ,-------10分
,-------10分∴
 .------------------12分
.------------------12分∴数列
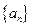 的前
的前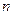 项和
项和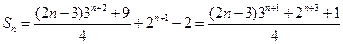

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,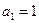 ,且当
,且当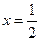 时,函数
时,函数
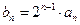 ,证明数列
,证明数列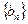 为等差数列;
为等差数列;
 项和为
项和为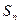 ,求
,求 
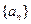 的前
的前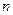 项和为
项和为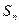 ,且
,且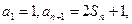 数列
数列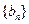 满足
满足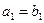 ,点
,点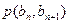 在直线
在直线 上,
上,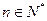 .
.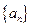 ,
,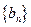 的通项公式;
的通项公式;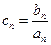 ,求数列
,求数列 的前
的前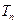 .
.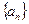 的前n项和记为
的前n项和记为 ,前
,前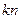 项和记为
项和记为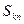
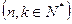 ,对给定的常数
,对给定的常数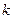 ,若
,若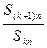 是与
是与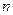 无关的非零常数
无关的非零常数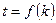 ,则称该数列
,则称该数列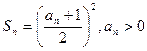 ,求数列
,求数列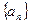 是一个 “
是一个 “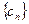 是一个等比数列,首项
是一个等比数列,首项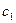 ,公比
,公比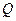
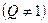 ,若数列
,若数列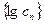 是一个 “
是一个 “ ( )
( )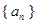 的前
的前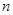 项和为
项和为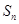 ,且
,且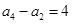 ,
,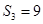 ,则数列
,则数列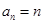
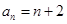
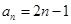
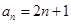
 ,
,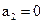 ,
,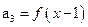 ,其中
,其中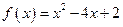 ,数列{an}前n项和存在最小值。
,数列{an}前n项和存在最小值。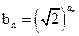 ,求数列
,求数列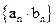 的前n项和
的前n项和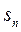
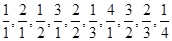 ,…依前10项的规律,这个数列的第2010项
,…依前10项的规律,这个数列的第2010项 满足( )
满足( )
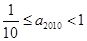


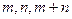 成等差数列,
成等差数列,  成等比数列, 则椭圆
成等比数列, 则椭圆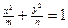 的准线方程为 ______
的准线方程为 ______