题目内容
已知数列{an}满足:a1=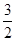 ,且an=
,且an=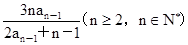
(1) 求数列{an}的通项公式;
(2) 证明:对于一切正整数n,不等式a1·a2·……an<2·n!
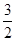 ,且an=
,且an=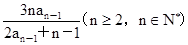
(1) 求数列{an}的通项公式;
(2) 证明:对于一切正整数n,不等式a1·a2·……an<2·n!
(1)an=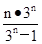 (n³1) (2)略
(n³1) (2)略
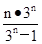 (n³1) (2)略
(n³1) (2)略本试题主要是考查了数列的通项公式的求解和数列求和的综合运用。
(1)因为将条件变为:1-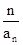 =
=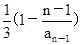 ,因此{1-
,因此{1-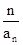 }为一个等比数列,其首项为1-
}为一个等比数列,其首项为1-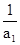 =
=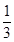 ,公比
,公比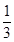 ,从而1-
,从而1-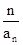 =
=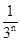 ,据此得an=
,据此得an=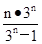 (n³1)
(n³1)
(2)据1°得,a1·a2·…an=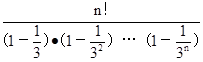
为证a1·a2·……an<2·n!
只要证nÎN*时有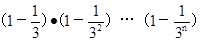 >
>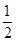 只要用数学归纳法证明即可。
只要用数学归纳法证明即可。
(1)因为将条件变为:1-
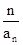 =
=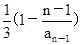 ,因此{1-
,因此{1-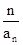 }为一个等比数列,其首项为1-
}为一个等比数列,其首项为1-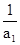 =
=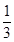 ,公比
,公比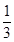 ,从而1-
,从而1-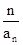 =
=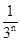 ,据此得an=
,据此得an=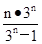 (n³1)
(n³1)(2)据1°得,a1·a2·…an=
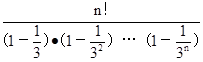
为证a1·a2·……an<2·n!
只要证nÎN*时有
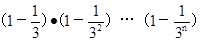 >
>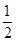 只要用数学归纳法证明即可。
只要用数学归纳法证明即可。
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的前
的前 项和为
项和为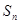 ,且
,且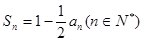
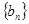 的通项公式
的通项公式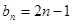 ,记
,记 ,求数列
,求数列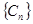 的前
的前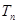 .
.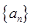 的通项公式是
的通项公式是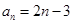 ,将数列中各项进行如下分组:第1组1个数(
,将数列中各项进行如下分组:第1组1个数(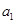 ),第2 组2个数(
),第2 组2个数(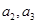 )第3组3个数(
)第3组3个数(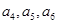 ),依次类推,……,则第16组的第10个数是 __________________.
),依次类推,……,则第16组的第10个数是 __________________.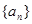 满足:
满足: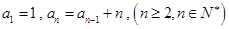 .
.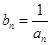 ,求数列
,求数列 的前
的前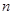 项和
项和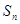 .
.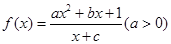 为奇函数,且
为奇函数,且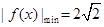 ,数列
,数列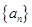 与
与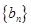 满足如下关系:
满足如下关系: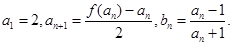
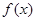 的解析式;
的解析式;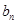 ;
;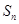 为数列
为数列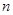 项和,求证:对任意的
项和,求证:对任意的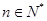 有
有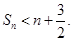
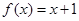 ,设
,设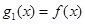 ,
,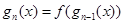
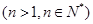 .
. 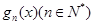 的表达式;此时若设
的表达式;此时若设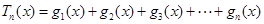 ,且关于
,且关于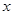 的函数
的函数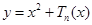
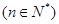 在区间
在区间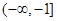 上的最小值为
上的最小值为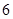 ,则求
,则求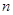 的值;
的值;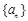 为等比数列,数列
为等比数列,数列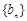 满足
满足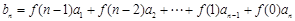 ,
,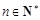 ,若
,若 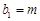 ,
,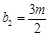 ,其中
,其中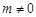 ,则
,则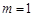 时,求
时,求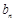 ;
;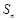 为数列
为数列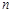 项和,若对于任意的正整数
项和,若对于任意的正整数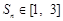 ,求实数
,求实数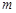 的取值范围.
的取值范围.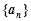 的前4项和为10,且
的前4项和为10,且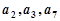 成等比数列.
成等比数列.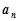 ;
;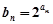 ,求数列
,求数列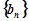 的前
的前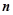 项和
项和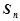 .
.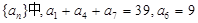 则数列
则数列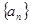 的前9项的和
的前9项的和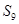 等于()
等于()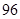
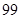
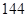
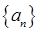 的前n项和为
的前n项和为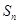 ,且
,且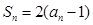 ,则
,则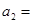 _______.
_______.