题目内容
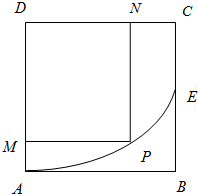 如图,ABCD是边长为4km的正方形地域,地域内有一条河流从A流到E,且河流是以A为顶点开口向上的一段抛物线弧,其中E为BC的中点.某公司准备投资建一个大型矩形游乐园PMDN,问如何修建才能使得游乐园的面积最大?最大面积是多少?
如图,ABCD是边长为4km的正方形地域,地域内有一条河流从A流到E,且河流是以A为顶点开口向上的一段抛物线弧,其中E为BC的中点.某公司准备投资建一个大型矩形游乐园PMDN,问如何修建才能使得游乐园的面积最大?最大面积是多少?
分析:首先建立坐标系,表示出抛物线AE的方程,并设P的坐标,用其坐标表示出游乐园的面积S的函数,通过求导法找到最大值.
解答: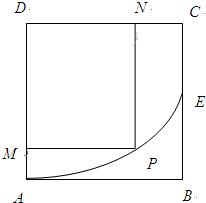 解:以A为原点,
解:以A为原点,
为x轴的正向建立平面直角坐标系.设抛物线弧AE
的方程为y=ax2(0≤x≤4)
∵E(4,2),2=16a?a=
,故y=
x2.
设P(x,
x2)(0<x≤4),矩形PMDN的面积为S,
则S=x(4-
x2)=-
x3+4x(0<x≤4).
∴S′=-
x2+4.
令S'=0,得x=
或x=-
(舍).
∵当x∈(0,
)
时,S'>0;当x∈(
,4)
时,S'<0,
∴x=
为S的极大值点,也是最大值点.
故当x=
时,S有最大值且最大值为S(
)=
.
答:当游乐园PMDN的两邻边MD=
km,DN=
km时,游乐园PMDN的面积最大,且最大面积等于
km2.
 解:以A为原点,
解:以A为原点,| AB |
的方程为y=ax2(0≤x≤4)
∵E(4,2),2=16a?a=
| 1 |
| 8 |
,故y=
| 1 |
| 8 |
设P(x,
| 1 |
| 8 |
则S=x(4-
| 1 |
| 8 |
| 1 |
| 8 |
∴S′=-
| 3 |
| 8 |
令S'=0,得x=
4
| ||
| 3 |
或x=-
4
| ||
| 3 |
∵当x∈(0,
4
| ||
| 3 |
时,S'>0;当x∈(
4
| ||
| 3 |
时,S'<0,
∴x=
4
| ||
| 3 |
为S的极大值点,也是最大值点.
故当x=
4
| ||
| 3 |
4
| ||
| 3 |
32
| ||
| 9 |
答:当游乐园PMDN的两邻边MD=
| 8 |
| 3 |
4
| ||
| 3 |
32
| ||
| 9 |
点评:本题考查根据实际问题选择函数类型,通过实际问题,抽象出函数模型,并通过求导计算最大值,考查对知识的综合运用能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
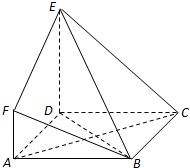 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.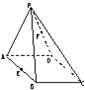 如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.
如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD. 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF. 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):