题目内容
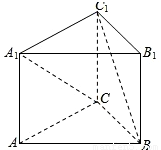如图，在正三棱柱ABC-A1B1C1中，侧棱长为
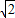，底面三角形的边长为2，则异面直线BC1与A1C所成的角是 ．
【答案】分析：如图所示，建立空间直角坐标系，利用异面直线的方向向量的夹角即可得到异面直线所成的角．
解答：解：建立如图所示的空间直角坐标系，点O，O1分别为边AC，A1C1的中点．
则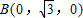
，C（-1，0，0），
，
．
∴
，
=
，
∴
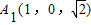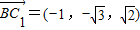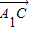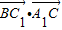=-2+0+2=0．
∴BC1⊥CA1．
∴异面直线BC1与A1C所成的角是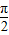
．
故答案是
．
点评：熟练掌握通过建立空间直角坐标系，利用异面直线的方向向量的夹角即可得到异面直线所成的角．
解答：解：建立如图所示的空间直角坐标系，点O，O1分别为边AC，A1C1的中点．
则
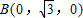，C（-1，0，0），，．∴
，=，∴
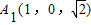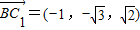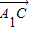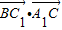=-2+0+2=0．∴BC1⊥CA1．
∴异面直线BC1与A1C所成的角是
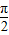．故答案是
．点评：熟练掌握通过建立空间直角坐标系，利用异面直线的方向向量的夹角即可得到异面直线所成的角．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，AB=1，若二面角C-AB-C1的大小为60°，则点C到平面C1AB的距离为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
如图，在正三棱柱ABC-A1B1C1中，D、E、G分别是AB、BB1、AC1的中点，AB=BB1=2．
如图，在正三棱柱ABC-A1B1C1中，AA1=4，AB=2，M是AC的中点，点N在AA1上，
（2012•马鞍山二模）如图，在正三棱柱ABC一DEF中，AB=2，AD=1，P是CF的延长线上一点，过A、B、P三点的平面交FD于M，交EF于N．