题目内容
在等比数列{an}中，首项a1＜0，则{an}是递增数列的充要条件是公比q满足（ ）A．q＞1
B．0＜q＜1
C．q＜1
D．q＜0
【答案】分析：先证必要性，由首项小于0，数列为递增数列，可得公比q大于0，得到数列的各项都小于0，利用等比数列的性质化简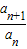
，得到其比值为q，根据其比值小于1，得到公比q小于1，综上，得到满足题意的q的范围；再证充分性，由0＜q＜1，首项为负数，得到数列各项都为负数，利用等比数列的性质化简
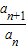，得到其比值为q，根据q小于1，得到an+1＞an，即数列为递增数列，综上，得到{an}是递增数列的充要条件是公比q满足0＜q＜1，得到正确的选项．
解答：解：先证必要性：
∵a1＜0，且{an}是递增数列，
∴an＜0，即q＞0，且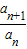
=
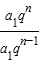=q＜1，
则此时等比q满足0＜q＜1，
再证充分性：
∵a1＜0，0＜q＜1，
∴an＜0，
∴
=
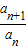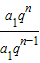=q＜1，即an+1＞an，
则{an}是递增数列，
综上，{an}是递增数列的充要条件是公比q满足0＜q＜1．
故选B
点评：此题考查了等比数列的性质，通项公式，以及充要条件的证明，熟练掌握等比数列的性质是解本题的关键．
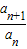，得到其比值为q，根据其比值小于1，得到公比q小于1，综上，得到满足题意的q的范围；再证充分性，由0＜q＜1，首项为负数，得到数列各项都为负数，利用等比数列的性质化简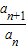，得到其比值为q，根据q小于1，得到an+1＞an，即数列为递增数列，综上，得到{an}是递增数列的充要条件是公比q满足0＜q＜1，得到正确的选项．解答：解：先证必要性：
∵a1＜0，且{an}是递增数列，
∴an＜0，即q＞0，且
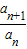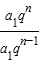==q＜1，则此时等比q满足0＜q＜1，
再证充分性：
∵a1＜0，0＜q＜1，
∴an＜0，
∴
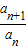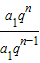==q＜1，即an+1＞an，则{an}是递增数列，
综上，{an}是递增数列的充要条件是公比q满足0＜q＜1．
故选B
点评：此题考查了等比数列的性质，通项公式，以及充要条件的证明，熟练掌握等比数列的性质是解本题的关键．
练习册系列答案
相关题目
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（ ）
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|