题目内容
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
【答案】B
【解析】解:设AC的中点为D,连接BD,PD,则PD⊥平面ABC, ∵△ABC是等腰直角三角形,∴外接球的球心O在PD上,
设AB=BC=a,PD=h,外接球半径OC=OP=R,
则OD=h﹣R,CD= ![]() AC=
AC= ![]() a,
a,
∵VP﹣ABC= ![]() =
= ![]() =
= ![]() ,∴a2=
,∴a2= ![]() ,
,
∵CD2+OD2=OC2 , 即(h﹣R)2+ ![]() a2=R2 ,
a2=R2 ,
∴R= ![]() =
= ![]() =
= ![]() ≥3
≥3 ![]() =
= ![]() ,
,
当且仅当 ![]() 即h=3时取等号,
即h=3时取等号,
∴当外接球半径取得最小值时,h=3.
故选:B.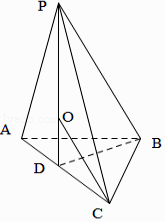
设AB=a,棱锥的高为h,根据体积得出a与h的关系,根据勾股定理得出外接球半径R关于h的表达式,利用基本不等式得出R最小值时对应的h的值即可.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
