题目内容
设F1,F2分别为双曲线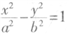 的左、右焦点,点P在双曲线右支上,但|PF2|=|F1F2|,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为
的左、右焦点,点P在双曲线右支上,但|PF2|=|F1F2|,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为
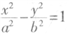 的左、右焦点,点P在双曲线右支上,但|PF2|=|F1F2|,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为
的左、右焦点,点P在双曲线右支上,但|PF2|=|F1F2|,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为[ ]
A.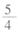
B.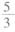
C.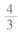
D.
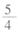
B.
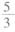
C.
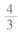
D.

B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
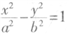 的左、右焦点,点P在双曲线右支上,但|PF2|=|F1F2|,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为
的左、右焦点,点P在双曲线右支上,但|PF2|=|F1F2|,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为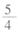
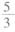
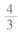


 阅读快车系列答案
阅读快车系列答案