题目内容
4.定义向量$\overrightarrow{OM}=({a,b})$的“相伴函数”为f(x)=asinx+bcosx;函数f(x)=asinx+bcosx的“相伴向量”为$\overrightarrow{OM}=({a,b})$(其中O为坐标原点).(1)若$g(x)=3sin({x+\frac{3π}{2}})+4sinx$,求g(x)的“相伴向量”;
(2)已知M(a,b)(b≠0)为圆C:(x-2)2+y2=1上一点,向量$\overrightarrow{OM}$的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围.
分析 (1)运用诱导公式和“相伴向量”的定义,即可得到;
(2)求得向量$\overrightarrow{OM}$的“相伴函数”f(x),求得最大值,及x0,运用正切的二倍角公式,以及函数y=x-$\frac{1}{x}$的单调性,和m=$\frac{b}{a}$的几何意义,即可得到所求范围.
解答 解:(1)$g(x)=3sin({x+\frac{3π}{2}})+4sinx$=4sinx-3cosx,
其相伴向量为$\overrightarrow{OM}=({4,-3})$;
(2)$\overrightarrow{OM}$的相伴函数为$f(x)=asinx+bcosx=\sqrt{{a^2}+{b^2}}sin({x+φ})$,
其中$cosφ=\frac{a}{{\sqrt{{a^2}+{b^2}}}}$,$sinφ=\frac{b}{{\sqrt{{a^2}+{b^2}}}}$,
当$x+φ=2kπ+\frac{π}{2}({k∈Z})$时,f(x)取到最大值,
故${x_0}=2kπ+\frac{π}{2}-φ$,$tan{x_0}=tan({2kπ+\frac{π}{2}-φ})=\frac{1}{tanφ}=\frac{a}{b}$,
$tan2{x_0}=\frac{{2×\frac{a}{b}}}{{1-{{({\frac{a}{b}})}^2}}}=\frac{2}{{\frac{b}{a}-\frac{a}{b}}}$,$m=\frac{b}{a}$为直线OM的斜率,
由几何意义知$m∈[{-\frac{{\sqrt{3}}}{3},0})∪({0,\frac{{\sqrt{3}}}{3}}]$,
当$-\frac{{\sqrt{3}}}{3}≤m<0$时,$tan2{x_0}=\frac{2}{{m-\frac{1}{m}}}$单调递减,所以$0<tan2{x_0}≤\sqrt{3}$;
当$0<m≤\frac{{\sqrt{3}}}{3}$时,$tan2{x_0}=\frac{2}{{m-\frac{1}{m}}}$单调递减,所以$-\sqrt{3}≤tan2{x_0}<0$,
所以$tan2{x_0}∈[{-\sqrt{3},0})∪({0,\sqrt{3}}]$.
点评 本题考查新定义的理解和运用,主要考查正弦函数的值域和直线的斜率及函数y=x-$\frac{1}{x}$的单调性,属于中档题.

| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 | a1 | a2 | a3 | a4 | a5 | a6 |

| x | 10 | 15 | 20 | 25 | 30 |
| y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A. | $\stackrel{∧}{y}$=0.63x-231.2 | B. | $\stackrel{∧}{y}$=0.56x+997.4 | C. | $\stackrel{∧}{y}$=50.2x+501.4 | D. | $\stackrel{∧}{y}$=60.4x+400.7 |
 的图象如右图所示,则下列函数图象正确的是( )
的图象如右图所示,则下列函数图象正确的是( )
 B.
B.
 D.
D.
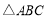 中,
中,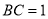 ,
,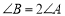 ,
,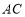 的取值范围为( )
的取值范围为( )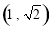 B.
B.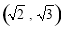
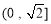 D.
D.