题目内容
(2013•宿迁一模)某商场在节日期间搞有奖促销活动,凡购买一定数额的商品,就可以摇奖一次.摇奖办法是在摇奖机中装有大小、质地完全一样且分别标有数字1~9的九个小球,一次摇奖将摇出三个小球,规定:摇出三个小球号码是“三连号”(如1、2、3)的获一等奖,奖1000元购物券;若三个小球号码“均是奇数或均是偶数”的获二等奖,奖500元购物券;若三个小球号码中有一个是“8”的获三等奖,奖200元购物券;其他情形则获参与奖,奖50元购物券.所有获奖等第均以最高奖项兑现,且不重复兑奖.记X表示一次摇奖获得的购物券金额.
(1)求摇奖一次获得一等奖的概率;
(2)求X的概率分布列和数学期望.
(1)求摇奖一次获得一等奖的概率;
(2)求X的概率分布列和数学期望.
分析:(1)记“摇奖一次获得一等奖”为事件A,连号的可能情况有:123,234,345,456,567,678,789共7种情况.由此能求出摇奖一次获得一等奖的概率.
(2)由题设知X的可能取值分别为1000,500,200,50.分别求出P(X=1000),P(X=500),P(X=200),P(X=50),由此能求出X的分布列EX.
(2)由题设知X的可能取值分别为1000,500,200,50.分别求出P(X=1000),P(X=500),P(X=200),P(X=50),由此能求出X的分布列EX.
解答:解:(1)记“摇奖一次获得一等奖”为事件A,
连号的可能情况有:123,234,345,456,567,678,789共7种情况.
∴P(A)=
=
=
.
故摇奖一次获得一等奖的概率为
.
(2)由题设知X的可能取值分别为1000,500,200,50.
P(X=1000)=
,P(X=500)=
=
,
P(X=200)=
=
,
P(X=50)=
=
=
,
∴X的分布列如下:
EX=
×1000+
×500+
×200+
×50=
.
连号的可能情况有:123,234,345,456,567,678,789共7种情况.
∴P(A)=
| 7 | ||
|
| 7 |
| 84 |
| 1 |
| 12 |
故摇奖一次获得一等奖的概率为
| 1 |
| 12 |
(2)由题设知X的可能取值分别为1000,500,200,50.
P(X=1000)=
| 1 |
| 12 |
| ||||
| 84 |
| 1 |
| 6 |
P(X=200)=
| ||||||
| 84 |
| 23 |
| 84 |
P(X=50)=
| ||||||
| 84 |
| 40 |
| 84 |
| 10 |
| 21 |
∴X的分布列如下:
| X | 1000 | 500 | 200 | 50 | ||||||||
| P |
|
|
|
|
| 1 |
| 12 |
| 1 |
| 6 |
| 23 |
| 84 |
| 10 |
| 21 |
| 5150 |
| 21 |
点评:本题考查离散型随机变量的分布列和数学期望的应用,是历年高考的必考题型之一.解题时要认真审题,仔细解答,注意排列组合和概率知识的灵活运用.

练习册系列答案
相关题目
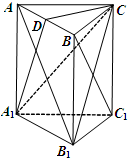 (2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.
(2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.