题目内容
（2013•宿迁一模）已知函数f（x）=||x-1|-1|，若关于x的方程f（x）=m（m∈R）恰有四个互不相等的实数根x1，x2，x3，x4，则x1x2x3x4的取值范围是
（-3，0）
（-3，0）
．分析：画出函数f（x）=||x-1|-1|的图象，可得方程f（x）=m（m∈R）恰有四个互不相等的实数根是地，m的取值范围，进而求出方程的四个根，进而根据m的范围和二次函数的图象和性质，可得x1x2x3x4的取值范围．
解答：解：函数f（x）=||x-1|-1|的图象如下图所示：
由图可知，若f（x）=m的四个互不相等的实数根，则m∈（0，1）
且x1，x2，x3，x4分别为：
x1=m，x2=2-m，x3=m+2，x4=-m，
∴x1x2x3x4=（m2）2-4•m2=（m2-2）2-4∈（-3，0）
故答案为：（-3，0）
由图可知，若f（x）=m的四个互不相等的实数根，则m∈（0，1）
且x1，x2，x3，x4分别为：
x1=m，x2=2-m，x3=m+2，x4=-m，
∴x1x2x3x4=（m2）2-4•m2=（m2-2）2-4∈（-3，0）
故答案为：（-3，0）
点评：本题考查的知识点是根的存在性及根的个数判断，其中画出函数的图象，引入数形结合思想是解答本题的关键
练习册系列答案
相关题目
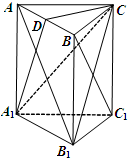（2013•宿迁一模）如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，BC=BB1，D为AB的中点．