Question

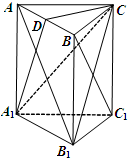（2013•宿迁一模）如图，在直三棱柱ABC-A₁B₁C₁中，AC⊥BC，BC=BB₁，D为AB的中点．
（1）求证：BC₁⊥平面AB₁C；
（2）求证：BC₁∥平面A₁CD．

Answer 1

分析：（1）BC₁⊥平面AB₁C，即要证BC₁与平面AB₁C内两条相交直线均垂直，结合已知、直棱柱的几何特征及正方形的性质，可证得结论．
（2）要证BC₁∥平面CA₁D，必须证明BC₁∥平面CA₁D内的一条直线，因而连接AC₁与A₁C的交点E与D，证明即可．

解答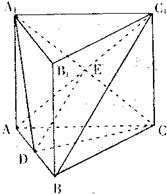：证明：（1）∵三棱柱ABC-A₁B₁C₁为直三棱柱
∴CC₁⊥平面ABC；
又∵AC?平面ABC
∴CC₁⊥AC
又∵AC⊥BC，CC₁∩BC=C
∴AC⊥平面B₁C₁CB
又∵B₁C?平面B₁C₁CB
∴B₁C⊥AC
又∵BC=BB₁，
∴平面B₁C₁CB为正方形，
∴B₁C⊥BC₁，又∵B₁C∩AC=C
∴BC₁⊥平面AB₁C；
（2）连接BC₁，连接AC₁于E，连接DE，E是AC₁中点，
D是AB中点，则DE∥BC₁，
又DE?面CA₁D₁，BC₁?面CA₁D₁
∴BC₁∥面CA₁D

点评：本题考查棱柱的结构特征，考查线面垂直的判定，线面平行的判定，转化的数学思想是中档题．