题目内容
若
+
+…+
=363,则自然数n=( )
| C | 23 |
| C | 24 |
| +C | 25 |
| C | 2n |
| A.11 | B.12 | C.13 | D.14 |
由C32+C42+C52+…+Cn2=363,
则1+C32+C42+C52+…+Cn2=364,即C33+C32+C42+C52+…+Cn2=364,
又由Cnm+Cnm-1=Cn+1m,则
+C32+C42+C52+…+Cn2=C43+C42+C52+…+Cn2=C53+C52+C62+…+Cn2=Cn+13,
原式可变形为Cn+13=364,
化简可得
=364,
又由n是正整数,解得n=13,
故选C.
则1+C32+C42+C52+…+Cn2=364,即C33+C32+C42+C52+…+Cn2=364,
又由Cnm+Cnm-1=Cn+1m,则
| C | 33 |
原式可变形为Cn+13=364,
化简可得
| (n+1)n(n-1) |
| 3×2×1 |
又由n是正整数,解得n=13,
故选C.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
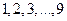 的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?