题目内容
已知椭圆
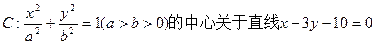 的对称点落在直线
的对称点落在直线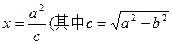 )上,且椭圆C的离心率为
)上,且椭圆C的离心率为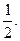
(1)求椭圆C的方程;
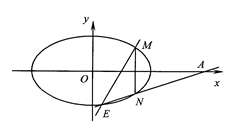
(2)设A(3,0),M、N是椭圆C上关于x轴对称的任意两点,连结AN交椭圆于另一点E,求证直线ME与x轴相交于定点.
(1) (2)直线ME与x轴相交于定点(
(2)直线ME与x轴相交于定点( ,0)
,0)
 (2)直线ME与x轴相交于定点(
(2)直线ME与x轴相交于定点( ,0)
,0)(1)
设O关于直线 的对称点为
的对称点为 ,
,
则 的横坐标为
的横坐标为
又易知直线O 的方程为
的方程为
为(1,-3).
∴椭圆方程为
(2)显然直线AN存在斜率,设直线AN的方程为
并整理得:
设点
由韦达定理得
∵直线ME方程为 的横坐标
的横坐标
将
再将韦达定理的结果代入,并整理可得
∴.

设O关于直线
 的对称点为
的对称点为 ,
,则
 的横坐标为
的横坐标为
又易知直线O
 的方程为
的方程为
为(1,-3).

∴椭圆方程为

(2)显然直线AN存在斜率,设直线AN的方程为

并整理得:

设点

由韦达定理得

∵直线ME方程为
 的横坐标
的横坐标
将

再将韦达定理的结果代入,并整理可得

∴.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
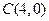 和直线
和直线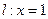 ,作
,作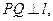 垂足为Q,且
垂足为Q,且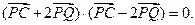
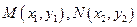
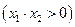 点
点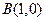 ,若
,若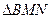 的面积为
的面积为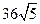 ,求直线
,求直线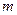 的方
的方 程.
程. .
. ;
; 是(1)中曲线
是(1)中曲线 的取值范围.
的取值范围. 中,射线
中,射线 在第一象限,且与
在第一象限,且与 轴的正半轴成定角
轴的正半轴成定角 ,动点
,动点 在射线
在射线 在
在 轴的正半轴上运动,
轴的正半轴上运动,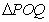 的面积为
的面积为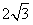 .
.
 中点
中点 的轨迹
的轨迹 的方程;
的方程; 是曲线
是曲线 ,
, 为
为 ,
, 恒成立?若存在,求出这个
恒成立?若存在,求出这个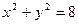 内有一点
内有一点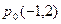 ,AB为过点
,AB为过点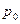 且倾斜角为α的弦,
且倾斜角为α的弦,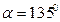 时,求AB的长;
时,求AB的长;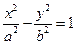 的离心率
的离心率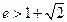 ,左、右焦点分别为
,左、右焦点分别为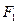 ,
,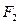 ,左准线为
,左准线为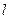 ,能否在双曲线的左支上找到一点
,能否在双曲线的左支上找到一点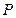 ,使得
,使得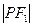 是
是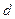 与
与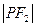 的等比中项?
的等比中项? 和圆O2:
和圆O2:  的位置关系是( )
的位置关系是( )