题目内容
【题目】已知两点
，直线AM，BM相交于点M，且这两条直线的斜率之积为
.
(1)求点M的轨迹方程；
(2)记点M的轨迹为曲线C，曲线C上在第一象限的点P的横坐标为1，过点P的斜率不为零且互为相反数的两条直线分别交曲线C于Q，R（异于点P），求直线QR的斜率.
【答案】（1）
（2）
【解析】
（1）设点
，通过
，即可求出曲线C的方程；
（2）把
代入曲线C的方程，可得
，直线PQ与直线PR的斜率互为相反数，设直线PQ的方程为
，与椭圆方程联立，由于是方程的一个解，所以方程的另一个解为
，同理
，可得直线QR的斜率.
(1)设点，因为，所以
，
整理得点所在的曲线C的方程为：
.
（2）由题意可得点，
直线PQ与直线PR的斜率互为相反数，设直线PQ的方程为，
与椭圆的方程联立消去y，得
，
由于是方程的一个解，所以方程的另一个解为，
同理，
故直线RQ的斜率为
.
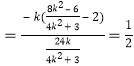练习册系列答案
相关题目
