题目内容
定义域为D的函数y=f(x),若存在常数a,b,使得对于任意x1,x2∈D,当x1+x2=2a时,总有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.已知函数f(x)=x3-3x2图象的对称中心的横坐标为1,则可求得: = .
= .
【答案】分析:函数f(x)=x3-3x2图象的对称中心的坐标为(1,-2),即x1+x2=2时,总有f(x1)+f(x2)=-4,再利用倒序相加,即可得到结论.
解答:解:由题意函数f(x)=x3-3x2图象的对称中心的坐标为(1,-2),即x1+x2=2时,总有f(x1)+f(x2)=-4
∴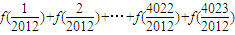 +
+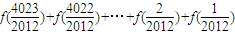 =-4×4023
=-4×4023
∴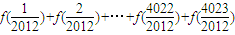 =-8046
=-8046
故答案为:-8046
点评:本题考查函数的对称性,确定函数的对称中心,利用倒序相加是关键.
解答:解:由题意函数f(x)=x3-3x2图象的对称中心的坐标为(1,-2),即x1+x2=2时,总有f(x1)+f(x2)=-4
∴
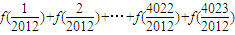 +
+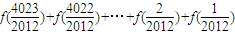 =-4×4023
=-4×4023∴
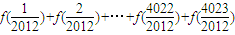 =-8046
=-8046故答案为:-8046
点评:本题考查函数的对称性,确定函数的对称中心,利用倒序相加是关键.

练习册系列答案
相关题目