题目内容
已知直线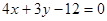 截圆心在点
截圆心在点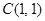 的圆
的圆 所得弦长为
所得弦长为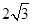 .
.
(1)求圆 的方程;
的方程;
(2)求过点 的圆
的圆 的切线方程.
的切线方程.
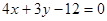 截圆心在点
截圆心在点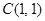 的圆
的圆 所得弦长为
所得弦长为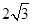 .
.(1)求圆
 的方程;
的方程; (2)求过点
 的圆
的圆 的切线方程.
的切线方程. (1)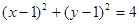
(2)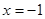 与
与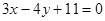
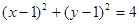
(2)
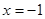 与
与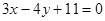
试题分析:(1)易知,圆心到直线的距离为
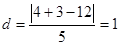 ,所以
,所以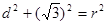 ,
,所以
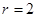 ,所以圆的方程为
,所以圆的方程为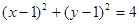 .
.(2)当斜率不存在时,易知直线
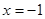 满足条件,当斜率存在时,设直线方程为
满足条件,当斜率存在时,设直线方程为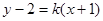 ,代入圆的方程得,
,代入圆的方程得,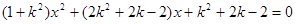 ,令
,令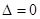 得
得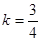 ,求得直线方程为
,求得直线方程为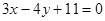 .故直线方程为
.故直线方程为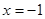 与
与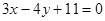 .
.点评:本题主要考查利用待定系数法求圆的方程,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
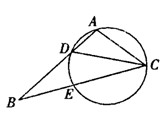
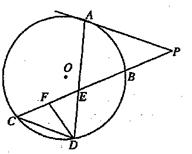
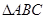 中,
中,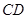 是
是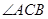 的角平分线,
的角平分线,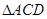 的外接圆交
的外接圆交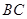 于
于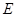 ,
,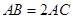 .
.
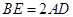 ;
;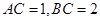 时,求
时,求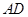 的长.
的长.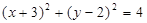 相切的直线方程是___________.
相切的直线方程是___________.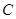 满足以下三个条件:(1)圆心在直线
满足以下三个条件:(1)圆心在直线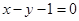 上,(2)与直线
上,(2)与直线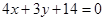 相切,(3)截直线
相切,(3)截直线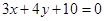 所得弦长为6。求圆
所得弦长为6。求圆 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )



 两点,圆心在x轴上,则圆C的方程是
两点,圆心在x轴上,则圆C的方程是



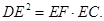

 轴上,且过两点
轴上,且过两点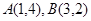 的圆的方程为 .
的圆的方程为 .