题目内容
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且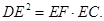
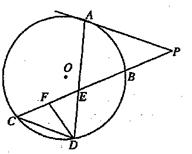
(1)求证:A、P、D、F四点共圆;
(2)若AE·ED=24,DE=EB=4,求PA的长。
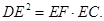

(1)求证:A、P、D、F四点共圆;
(2)若AE·ED=24,DE=EB=4,求PA的长。
(1)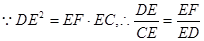 又
又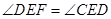 ,
, 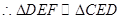 ,
,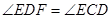 又
又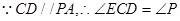 故
故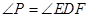 所以
所以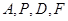 四点共圆
四点共圆
(2)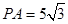
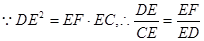 又
又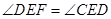 ,
, 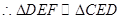 ,
,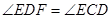 又
又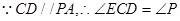 故
故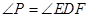 所以
所以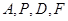 四点共圆
四点共圆(2)
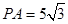
试题分析:(1)证明:
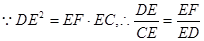 ,
,又
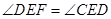 ,
, 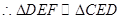 ,
,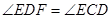 ,
,又
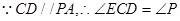 故
故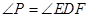 ,
,所以
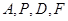 四点共圆. 5分
四点共圆. 5分(2)解:由(Ⅰ)及相交弦定理得
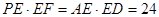 ,
,又
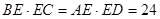 ,
, ,
,由切割线定理得
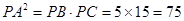 ,
,所以
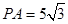 为所求. 10分
为所求. 10分点评:证明四点共圆可证明四边形对角互补,求切线段长度可借助于切割线定理将其转化为割线长度

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
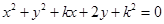 所表示的圆取得最大面积时,则直线
所表示的圆取得最大面积时,则直线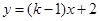 的倾斜角
的倾斜角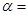 ( ).
( ).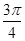
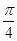
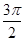
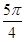
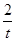 )(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若
)(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若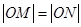 ,则圆C的方程 .
,则圆C的方程 .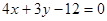 截圆心在点
截圆心在点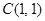 的圆
的圆 所得弦长为
所得弦长为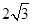 .
. 的圆
的圆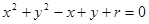 表示一个圆,则
表示一个圆,则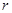 的取值范围是( )
的取值范围是( ) 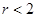
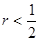
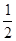
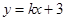 与圆
与圆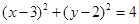 相交于
相交于 ,
, 两点,且
两点,且 ,则
,则 的取值范围是( )
的取值范围是( )
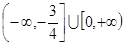

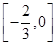
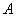 ,
,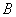 ,
,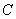 ,
,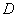 四点共圆,
四点共圆,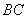 与
与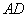 的延长线交于点
的延长线交于点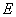 ,点
,点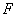 在
在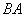 的延长线上.
的延长线上.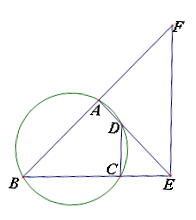
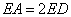 ,
,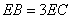 ,求
,求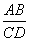 的值;
的值;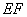 ∥
∥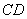 ,求证:线段
,求证:线段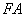 ,
,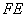 ,
,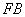 成等比数列.
成等比数列.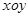 中,已知圆
中,已知圆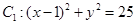 和圆
和圆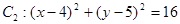 .
.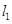 经过点
经过点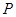 (2,-1)和圆
(2,-1)和圆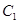 的圆心,求直线
的圆心,求直线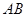 的中点,求直线
的中点,求直线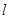 过点
过点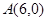 ,且被圆
,且被圆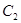 截得的弦长为
截得的弦长为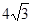 ,求直线
,求直线 的方程.
的方程.