题目内容
已知圆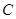 满足以下三个条件:(1)圆心在直线
满足以下三个条件:(1)圆心在直线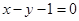 上,(2)与直线
上,(2)与直线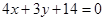 相切,(3)截直线
相切,(3)截直线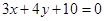 所得弦长为6。求圆
所得弦长为6。求圆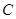 的方程。
的方程。
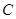 满足以下三个条件:(1)圆心在直线
满足以下三个条件:(1)圆心在直线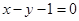 上,(2)与直线
上,(2)与直线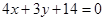 相切,(3)截直线
相切,(3)截直线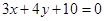 所得弦长为6。求圆
所得弦长为6。求圆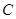 的方程。
的方程。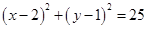
试题分析:∵圆心C在直线x-y-1=0上,∴圆心C(a,a-1),又圆
与直线
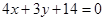 相切,截直线
相切,截直线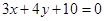 所得弦长为6所以,
所得弦长为6所以,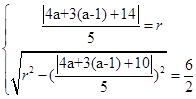 ,解得,
,解得,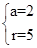 ,故圆
,故圆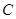 的方程
的方程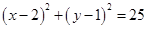 。
。点评:中档题,求圆的方程,可以根据条件灵活假设出方程的形式,一般地,涉及圆心、半径时,设标准方程,涉及圆上点的坐标时,设一般形式。本题对计算能力要求较高。

练习册系列答案
相关题目
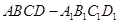 的棱长为2,点
的棱长为2,点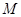 是
是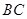 的中点,点
的中点,点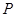 是正方形
是正方形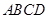 所在平面内的一个动点,且满足
所在平面内的一个动点,且满足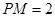 ,
,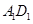 的距离为
的距离为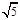 ,则点
,则点 的一个焦点为圆心,离心率为半径的圆的方程是( )
的一个焦点为圆心,离心率为半径的圆的方程是( )


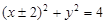
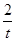 )(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若
)(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若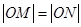 ,则圆C的方程 .
,则圆C的方程 .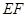 的长度为1,端点
的长度为1,端点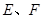 在边长为2的正方形
在边长为2的正方形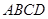 的四边上滑动.当
的四边上滑动.当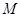 所形成的轨迹为
所形成的轨迹为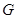 ,若
,若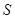 ,则
,则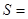 .
.
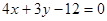 截圆心在点
截圆心在点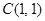 的圆
的圆 所得弦长为
所得弦长为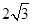 .
. 的圆
的圆