题目内容
【题目】已知a∈R,函数f(x)=x|x﹣a|.
(1)当a=2时,将函数f(x)写成分段函数的形式,并作出函数的简图,写出函数y=f(x)的单调递增区间;
(2)当a>2时,求函数y=f(x)在区间[1,2]上的最小值.
【答案】
(1)解:当a=2时,f(x)=x|x﹣2|= ![]() ,
,
故作其图象如右图,
函数y=f(x)的单调递增区间为(﹣∞,1],(2,+∞);
(2)解:f(x)= ![]() ,
,
①当1< ![]() <2,即2<a<4时,
<2,即2<a<4时,
f(x)在[1, ![]() ]上是增函数,在(
]上是增函数,在( ![]() ,2]上是减函数;
,2]上是减函数;
而f(1)=a﹣1,f(2)=2a﹣4,
故f(1)﹣f(2)=a﹣1﹣2a+4=3﹣a,
故当2<a≤3时,
f(1)≥f(2),
故fmin(x)=f(2)=2a﹣4;
当3<a<4时,
f(1)<f(2),
故fmin(x)=f(1)=a﹣1;
②当a≥4时,f(x)在[1,2]上是增函数,
故fmin(x)=f(1)=a﹣1;
综上所述,fmin(x)= ![]() .
.
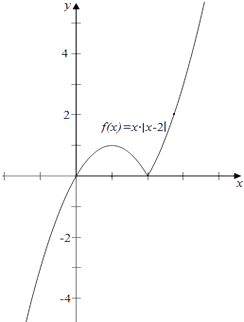
【解析】(1)化简f(x)=x|x﹣2|= ![]() ,从而作其图象,并写出单调增区间;(2)化简f(x)=
,从而作其图象,并写出单调增区间;(2)化简f(x)= ![]() ,分类讨论以确定函数的单调性,从而比较以确定函数的最小值.
,分类讨论以确定函数的单调性,从而比较以确定函数的最小值.
【考点精析】掌握二次函数在闭区间上的最值是解答本题的根本,需要知道当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
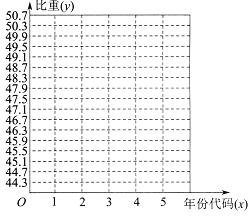
【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
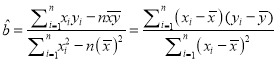 ,
, ![]() .
.