题目内容
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() (
(![]() );数列
);数列![]() 为等差数列.且
为等差数列.且![]() ,
,![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若![]() 为数列
为数列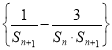 的前n项和,求满足不等式
的前n项和,求满足不等式![]() 的n的最大值.
的n的最大值.
【答案】(1)![]() ,
,![]() (2)9
(2)9
【解析】
(1)根据等式![]() ,令
,令![]() ,可求出
,可求出![]() ,再当
,再当![]() ≥
≥![]() 时,由
时,由![]() 可得
可得![]() ,再结合
,再结合![]() 可确定数列
可确定数列![]() 的通项公式,即可得
的通项公式,即可得![]() 和
和![]() 的值,进而得到
的值,进而得到![]() 和
和![]() 的值,因为数列
的值,因为数列![]() 为等差数列,可求出公差d,然后得出数列
为等差数列,可求出公差d,然后得出数列![]() 通项公式;(2)先根据数列
通项公式;(2)先根据数列![]() 的通项公式求出
的通项公式求出![]() ,再表示出
,再表示出![]() ,然后用裂项相消法求出数列
,然后用裂项相消法求出数列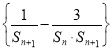 的前n项和
的前n项和![]() ,最后判断满足不等式
,最后判断满足不等式![]() 的n的最大值.
的n的最大值.
解:(1)因为![]() ,所以当
,所以当![]() 时,
时,![]() ,解得
,解得![]() .
.
当![]() ≥
≥![]() 时,
时,![]() ,化简得
,化简得![]() .
.
又![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
所以![]() 是首项为
是首项为![]() 公比为2的等比数列,即
公比为2的等比数列,即![]() ;
;
又![]() ,
,![]() ,即
,即![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
因为数列![]() 为等差数列,所以公差
为等差数列,所以公差![]() ,故
,故![]() ;
;
(2)由(1)知![]() 是首项为
是首项为![]() 公比为2的等比数列,所以
公比为2的等比数列,所以![]() ,
,
所以![]()
![]()
![]()
![]()
![]() ,
,
故![]()
![]()
![]() .
.
若![]() ,即
,即![]() ,即
,即![]() ,
,
可得![]() ,所以
,所以![]() ,
,
综上,使得![]() 的最大的
的最大的![]() 的值为9.
的值为9.

 阅读快车系列答案
阅读快车系列答案【题目】十八大以来,我国新能源产业迅速发展.以下是近几年某新能源产品的年销售量数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源产品年销售 | 1.6 | 6.2 | 17.7 | 33.1 | 55.6 |
(1)请画出上表中年份代码![]() 与年销量
与年销量![]() 的数据对应的散点图,并根据散点图判断.
的数据对应的散点图,并根据散点图判断.
![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年份代码
关于年份代码![]() 的回归方程类型;
的回归方程类型;
(2)根据(Ⅰ)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
参考公式: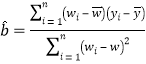 ,
,![]() .
.
参考数据: ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
【题目】公历![]() 月
月![]() 日为我国传统清明节,清明节扫墓我们都要献鲜花,某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花,具体价格统计如下表所示
日为我国传统清明节,清明节扫墓我们都要献鲜花,某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花,具体价格统计如下表所示
日供应量 |
|
|
|
|
|
|
单位 |
|
|
|
|
|
|
(I)根据上表中的数据进行判断,函数模型![]() 与
与![]() 哪一个更适合于体现日供应量
哪一个更适合于体现日供应量![]() 与单价
与单价![]() 之间的关系;(给出判断即可,不必说明理由)
之间的关系;(给出判断即可,不必说明理由)
(II)根据(I)的判断结果以及参考数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(III)该地区有![]() 个商店,其中
个商店,其中![]() 个商店每日对这种鲜花的需求量在
个商店每日对这种鲜花的需求量在![]() 束以下,
束以下,![]() 个商店每日对这种鲜花的需求量在
个商店每日对这种鲜花的需求量在![]() 束以上,则从这
束以上,则从这![]() 个商店个中任取
个商店个中任取![]() 个进行调查,求恰有
个进行调查,求恰有![]() 个商店对这种鲜花的需求量在
个商店对这种鲜花的需求量在![]() 束以上的概率.
束以上的概率.
参考公式及相关数据:对于一组数据![]() ,
,![]() ,...,
,...,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为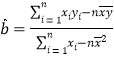 ,
,![]() .
.
|
|
|
|
|
|
|
|
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研究投入.为了对新研发的产品进行合理定价,将该产品按事先拟定的价格试销,得到一组检测数据如表所示:
试销价格 |
|
|
|
|
|
|
产品销量 |
|
|
|
|
|
|
已知变量![]() ,
,![]() 具有线性相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲/span>
具有线性相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲/span>![]() ;乙
;乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?求回归方程。
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”.现从检测数据中随机抽取3个,求“理想数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.