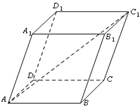
题目内容
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=
,P是BC1上一动点,则A1P+PC的最小值是______.

| 3 |

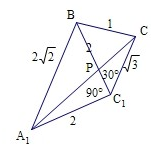
连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,如图所示,
连A1C,则A1C的长度就是所求的最小值.
在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=
,
∴BC1=2,A1C1=2,A1B=2
,BC=1,CC1=
,
即∠A1C1B=90°,∠CC1B=30°,
∴∠A1C1C=90°+30°=120°,
由余弦定理可求得A1C2=22+(
)2-2×2×
×cos120°=4+3+2×2×
×
=7+2
,
∴A1P+PC的最小值是
,
故答案为:
.
连A1C,则A1C的长度就是所求的最小值.
在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=
| 3 |
∴BC1=2,A1C1=2,A1B=2
| 2 |
| 3 |
即∠A1C1B=90°,∠CC1B=30°,
∴∠A1C1C=90°+30°=120°,
由余弦定理可求得A1C2=22+(
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
∴A1P+PC的最小值是
7+2
|
故答案为:
7+2
|


练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目