Question

【题目】将函数的图象向右平移（）个单位长度后得到函数的图象，若在区间上单调递增，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】分析：根据平移关系求出g（x）的解析式，结合函数的单调性建立不等式关系进行求解即可．

详解：将函数f（x）=sin2x的图象向右平移φ（0＜＜）个单位长度后得到函数g（x）的图象，

则g（x）=sin2（x﹣）=sin（2x﹣2），

若g（x）在区间[0，]上单调递增，

则2kπ﹣≤2x﹣2≤2kπ+，k∈Z，

得2kπ﹣+2≤2x≤2kπ++2，k∈Z，

即kπ﹣+≤x≤kπ++，k∈Z，

即函数的单调递增区间为[kπ﹣+，kπ++]，k∈Z，

∵若g（x）在区间[0，]上单调递增，

∴满足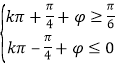，即，

则﹣kπ﹣≤≤﹣kπ+，k∈Z，

当k=0时，﹣≤≤，

又因为：0＜＜

所以的取值范围是（0，]，

故选：D．