题目内容
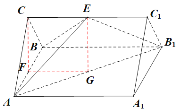
【题目】如图，在三棱柱
中，底面ABC为正三角形，
底面ABC，
，点
在线段
上，平面
平面
．
（1）请指出点的位置，并给出证明；
（2）若
，求
与平面ABE夹角的正弦值．
【答案】（1）见解析；
（2）
.
【解析】
（1）取
中点为
，
的中点为
，连接
，
，
．四边形
为平行四边形,即可说明
平面
，即
平面，即平面
平面.
（2）利用等体积法
，即可求出点
到平面ABE的距离的
，再代入公式
，即可求出答案。
（1）点
为线段
的中点．
证明如下：取中点为，的中点为，连接，，．
所以
，
，所以四边形为平行四边形．所以
．
因为
，
，所以
．
又因为
平面
，
平面，所以
．
又
，所以平面．
所以平面，而
平面
，所以平面平面.
（2）由
，得
．
由（1）可知，点到平面
的距离为
．
而
的面积
，
等腰
底边AB上的高为
记点到平面ABE的距离为，
由
，得
，
即点到平面ABE的距离为
.又
与平而ABE夹角的正弦值
.
【题目】二手车经销商小王对其所经营的
型号二手汽车的使用年数
与销售价格
（单位：万元/辆）进行整理，得到如下数据：
使用年数 |
|
|
|
|
|
|
售价 |
|
|
|
|
|
|
|
|
|
|
|
|
|
下面是
关于的折线图：
（1）由折线图可以看出，可以用线性回归模型拟合与的关系，请用相关系数加以说明；
（2）求关于的回归方程并预测某辆型号二手车当使用年数为
年时售价约为多少？（
、
小数点后保留两位有效数字）
（3）基于成本的考虑，该型号二手车的售价不得低于
元，请根据（2）求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年？
参考数据：
，
，
，
，
，
，
，
.
参考公式：回归直线方程
中斜率和截距的最小二乘估计公式分别为：
，
.
，
、
为样本平均值.
【题目】为响应绿色出行，某市在推出“共享单车”后，又推出“新能源分时租赁汽车”．其中一款新能源分时租赁汽车，每次租车收费的标准由两部分组成：①根据行驶里程数按1元/公里计费；②行驶时间不超过
分时，按
元/分计费；超过分时，超出部分按
元/分计费．已知王先生家离上班地点15公里，每天租用该款汽车上、下班各一次．由于堵车、红绿灯等因素，每次路上开车花费的时间
(分)是一个随机变量．现统计了50次路上开车花费时间，在各时间段内的频数分布情况如下表所示：
时间 |
|
|
|
|
频数 | 2 | 18 | 20 | 10 |
将各时间段发生的频率视为概率，每次路上开车花费的时间视为用车时间，范围为
分．
（1）写出王先生一次租车费用
（元）与用车时间（分）的函数关系式；
（2）若王先生一次开车时间不超过40分为“路段畅通”，设
表示3次租用新能源分时租赁汽车中“路段畅通”的次数，求的分布列和期望；
（3）若公司每月给1000元的车补，请估计王先生每月（按22天计算）的车补是否足够上、下班租用新能源分时租赁汽车？并说明理由．（同一时段，用该区间的中点值作代表）
