题目内容
7.如果→a、→b是非零向量,则下列命题中正确的是( )| A. | →a•→b=0⇒→a=→0或→b=→0 | B. | →a∥→b⇒→a在→b上投影为|→a| | ||
| C. | →a⊥→b⇒→a•→b=(→a•→b)2 | D. | →a•→c=→b•→c⇒→a=→b |
分析 根据向量垂直的充要条件,可判断A,C;根据向量投影的定义,可判断B;根据向量数量积的几何意义,可判断D.
解答 解:∵→a•→b=0?→a⊥→b,故A错误,C正确;
若→a∥→b⇒→a在→b上投影为±|→a|(同向为|→a|,反向为-|→a|),故B错误;
若→a•→c=→b•→c,则→a,→b在→c上的投影相等,但→a=→b不一定成立,故D错误;
故选:C
点评 本题以命题的真假判断为载体,考查了命题的真假判断与应用,难度不大,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.Sn=1+(1+12)+(1+12+14)+…(1+12+14+…+12n−1)等于( )
| A. | 12n | B. | 2n+12n−1 | C. | 2n-2+12n−1 | D. | n−12n−1 |
11.记f(x)=1+x1−x,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2015(x)=( )
| A. | -1x | B. | x | C. | x−1x+1 | D. | 1+x1−x |
2.下列说法错误的是( )
| A. | 在独立性检验中,K2的值越大,说明确定两个量有关系的把握越大 | |
| B. | 计算误差,测量误差都将影响到残差的大小 | |
| C. | 在回归分析中R2的值越大,说明拟合效果越好 | |
| D. | 球的体积与它的半径具有相关关系 |
17.设a,b是空间两条垂直的直线,且b∥平面α,则在“a∥α”“a?α”“a∩α”中,能够出现的情况有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
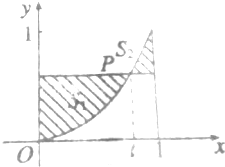 如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.
如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.