题目内容
 (本题满分12分)如图,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足
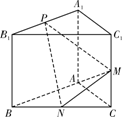
(本题满分12分)如图,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足![]() .
.
(1)证明:PN⊥AM;
(2)若平面PMN与平面ABC所成的角为45°,试确定点P的位置.
解:(1)证明:如图,以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz.
则P(λ,0,1),N(,,0),M(0,1,),…………………2分
 从而
从而![]() =(-λ,,-1),
=(-λ,,-1),![]() =(0,1,),
=(0,1,),![]() =(-λ)×0+×1-1×=0,所以PN⊥AM.…………………4分
=(-λ)×0+×1-1×=0,所以PN⊥AM.…………………4分
(2)平面ABC的一个法向量为n=![]() =(0,0,1).
=(0,0,1).
设平面PMN的一个法向量为m=(x,y,z),
由(1)得![]() =(λ,-1,).
=(λ,-1,).
由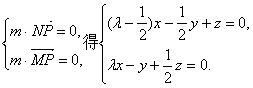 ………………6分
………………6分
解得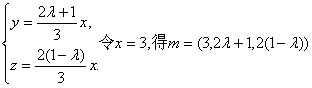 .……………8分
.……………8分
∵平面PMN与平面ABC所成的二面角为45°,
∴|cos〈m,n〉|=||==,
解得λ=-.…………………10分
故点P在B1A1的延长线上,且|A1P|=.…………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
