题目内容
5.设函数f(x)=lnx+$\frac{a}{x}$-a.(1)讨论函数f(x)的单调性并求函数f(x)的极值;
(2)若h(x)=f(x+1),当a>0时,若对任意的x≥0,恒有h(x)≥0,求实数a的取值范围;
(3)设x∈N,且x>2,试证明:lnx>$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{x}$.
分析 (1)求出函数的定义域,f′(x)=0,分a≤0,a>0两种情况讨论,由f′(x)的符号可判断函数单调性,根据单调性可判断函数极值;
(2)对任意的x≥0,恒有h(x)≥0等价于h(x)min≥0,按0<a≤1,a>1两种情况讨论,借助(1)问结论可求得函数h(x)的最小值;
(3)由(2)可知,ln(1+x)≥$\frac{x}{x+1}$,则lnx=ln($\frac{2}{1}$×$\frac{3}{2}$×…×$\frac{x}{x-1}$)=ln2+ln$\frac{3}{2}$+…+ln$\frac{x}{x-1}$=ln(1+1)+ln(1+$\frac{1}{2}$)+…+ln(1+$\frac{1}{x-1}$),利用不等式进行放缩,整理可得结论.
解答 解:(1)函数f(x)的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
①当a≤0时,恒有x-a>0,恒有f′(x)>0,f(x)在(0,+∞)上单调递增,无极值;
②当a>0时,由f′(x)=0得x=a,
当x∈(0,a)时,f′(x)<0,当x∈(a,+∞)时,f′(x)>0,
故函数f(x)在(0,a)上单调递减,在(a,+∞)上单调递增,
故当x=a时f(x)取得极小值,无极大值,极小值为f(a)=lna+1-a.
(2)h(x)=f(x+1)=ln(x+1)+$\frac{a}{x+1}$-a,
当0<a≤1时,y=h(x)在(0,+∞)上单调递增,h(x)≥h(0)=0,所以满足题意;
当a>1时,由(1)可知应有h(a-1)=lna+1-a≥0(*)成立,
令g(a)=lna+1-a,则g′(a)=$\frac{1}{a}$-1,g′(a)<0,g(a)在(1,+∞)上单调递减,
所以g(a)<0,即h(a-1)=g(a)<0,与(*)不符,
所以a的取值范围是0<a≤1.
(3)由(2)可知,ln(1+x)≥$\frac{x}{x+1}$,
所以lnx=ln($\frac{2}{1}$×$\frac{3}{2}$×…×$\frac{x}{x-1}$)=ln2+ln$\frac{3}{2}$+…+ln$\frac{x}{x-1}$=ln(1+1)+ln(1+$\frac{1}{2}$)+…+ln(1+$\frac{1}{x-1}$)
>$\frac{1}{2}$+$\frac{\frac{1}{2}}{1+\frac{1}{2}}$+…+$\frac{\frac{1}{x-1}}{1+\frac{1}{x-1}}$=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{x}$.
点评 题考查利用导数研究函数的极值、在闭区间上的最值,考查不等式的证明,考查分类讨论思想,考查解决问题的能力,解决(3)问的关键是借助(2)得到不等式,然后对lnx进行恰当变形.

| A. | 3$\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 3 |
| A. | $\frac{13}{16}$ | B. | $\frac{4}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
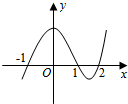 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(1)和极小值f(-1) | B. | 函数f(x)有极大值f(1)和极小值f(2) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(1) | D. | 函数f(x)有极大值f(-1)和极小值f(2) |
| A. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\vec a+\vec b-\frac{1}{2}\vec c$ | C. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\vec c$ | D. | $\frac{1}{2}\vec a+\vec b-\frac{1}{2}\vec c$ |
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |