题目内容
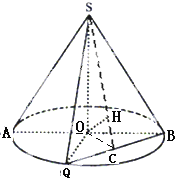
【题目】如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.

(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(Ⅱ)连接OC、AQ,由三角形中位线定理可得OC∥AQ,由圆周角定理我们可得OC⊥BQ,由圆锥的几何特征,可得SO⊥BQ,进而由线面垂直的判定定理,得到QB⊥平面SOC,则OH⊥BQ,结合OH⊥SC及线面垂直的判定定理得到OH⊥平面SBQ;(Ⅱ)若∠AOQ=60°,易得∠OBQ=∠OQB=30°,又由![]() 我们求出圆锥的底面半径OA长及圆锥的高SO,即可得到圆锥的体积及表面积.
我们求出圆锥的底面半径OA长及圆锥的高SO,即可得到圆锥的体积及表面积.
试题解析:(1)连接OC,∵SQ=SB,OQ=OB,QC=CB,
∴QB⊥SC,QB⊥OC,∴QB⊥平面SOC.
∵OH平面SOC,∴QB⊥OH,
又∵OH⊥SC,∴OH⊥平面SQB.
(2)连接AQ.∵Q为底面圆周上的一点,AB为直径,
∴AQ⊥QB.
在Rt△AQB中,∠QBA=30°,QB=2![]() ,
,
∴AB=![]() =4.
=4.
∵△SAB是等腰直角三角形,∴SO=![]() AB=2,
AB=2,
∴V圆锥=![]() π·OA2·SO=
π·OA2·SO=![]() .
.
S侧=![]() .
.

练习册系列答案
相关题目